��Ŀ����
16����ֱ֪��a��b����A��ֱ��a�ϣ���B��Cֱ��b�ϣ���D���߶�BC�ϣ���1����ͼ��ABƽ�֡�MAD��ACƽ�֡�NAD��DE��AC��E����֤����1=��2��
��2������FΪ�߶�AB�ϲ���A��B�غϵ�һ���㣬��H��AC�ϣ�FQƽ�֡�AFD��AC��Q�����HFQ=x�㣬����ʱ��DΪ�߶�BC�ϲ����B��C�غϵ���һ�㣩���ʵ������£�x֮�����������ĵ�����ϵʱ��FH��a�����Դ�Ϊ����֤��FH��a��
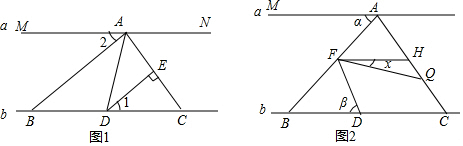
���� ��1���ȸ���a��b�ó���2=��ABD������ABƽ�֡�MAD��ACƽ�֡�NAD�ɵó���BAC=90�㣬����
DE��AC��֪��DEC=90�㣬��AB��DE���ݴ˿ɵó����ۣ�
��2���ȸ�������ó����ۣ�����ƽ���ߵ��ж����������жϼ��ɣ�
��� ��1��֤������a��b��
���2=��ABD��
��ABƽ�֡�MAD��ACƽ�֡�NAD��
���BAC=90�㣮
��DE��AC��
���DEC=90�㣬
��AB��DE��
���ABD=��1��
���2=��1��
��2���⣺����-��=2xʱ��FH��a��
���ɣ���a��b��
��Ϧ�=��ABD��
�ߡ�AFD�ǡ�BDF����ǣ�
���ABD+�Ϧ�=��AFD������+��=��AFD��
��FQƽ�֡�AFD��AC��Q��
���AFQ=��DFQ=$\frac{1}{2}$����+�£���
�ߡ�AFQ=��AFH+x=��DFQ-x��
���DFQ-��AFH=2x��
�ߦ�-��=2x��
���AFH=����
��FH��a��
���� ���⿼�����ƽ���ߵ��ж������ʣ���֪ƽ���ߵ��ж������ǽ�����Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
7�����з��������Ƕ�Ԫһ�η�������ǣ�������
| A�� | $\left\{\begin{array}{l}{x-y=3}\\{xy=1}\end{array}\right.$ | B�� | $\left\{\begin{array}{l}{2x+y=5}\\{x=3y-2}\end{array}\right.$ | C�� | $\left\{\begin{array}{l}{{x}^{2}-y=1}\\{y=2x}\end{array}\right.$ | D�� | $\left\{\begin{array}{l}{\frac{1}{y}-\frac{1}{x}=2}\\{x+y=0}\end{array}\right.$ |
3����x=0�ǹ���x��һԪ���η��̣�a+2��x2-$\sqrt{a-2}$x+a2+a-6=0��һ��������a��ֵ�ǣ�������
| A�� | a��-2 | B�� | a=2 | C�� | a=-3 | D�� | a=-3��a=2 |
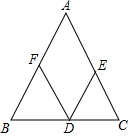 ��ͼ��D�ǵ���������ABC�ĵױ�BC�ϵ�һ�㣬E��F�ֱ���AC��AB�ϣ���DE��AB��DF��AC������DE��DF��AB֮����ʲô��ϵ����˵�����ɣ�
��ͼ��D�ǵ���������ABC�ĵױ�BC�ϵ�һ�㣬E��F�ֱ���AC��AB�ϣ���DE��AB��DF��AC������DE��DF��AB֮����ʲô��ϵ����˵�����ɣ�
 ��ͼ��ʾ�������߶�6������������7����
��ͼ��ʾ�������߶�6������������7����