题目内容
12.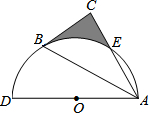 如图,B,E是以AD为直径的半圆O的三等分点,弧BE的长为$\frac{2}{3}$π,∠C=90°,则图中阴影部分的面积为( )
如图,B,E是以AD为直径的半圆O的三等分点,弧BE的长为$\frac{2}{3}$π,∠C=90°,则图中阴影部分的面积为( )| A. | $\frac{π}{9}$ | B. | $\frac{{\sqrt{3}π}}{9}$ | C. | $\frac{{3\sqrt{3}}}{2}-\frac{2π}{3}$ | D. | $\frac{{3\sqrt{3}}}{2}-\frac{{\sqrt{3}π}}{2}$ |
分析 首先根据圆周角定理得出扇形半径以及圆周角度数,进而利用锐角三角函数关系得出BC,AC的长,利用S△ABC-S扇形BOE=图中阴影部分的面积求出即可.
解答 解:连接BD,BE,BO,EO,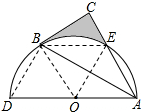
∵B,E是半圆弧的三等分点,
∴∠EOA=∠EOB=∠BOD=60°,
∴∠BAC=∠EBA=30°,
∴BE∥AD,
∵弧BE的长为$\frac{2}{3}$π,
∴$\frac{60π×R}{180}$=$\frac{2}{3}$π,
解得:R=2,
∴AB=ADcos30°=2$\sqrt{3}$,
∴BC=$\frac{1}{2}$AB=$\sqrt{3}$,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=3,
∴S△ABC=$\frac{1}{2}$×BC×AC=$\frac{1}{2}$×$\sqrt{3}$×3=$\frac{3\sqrt{3}}{2}$,
∵△BOE和△ABE同底等高,
∴△BOE和△ABE面积相等,
∴图中阴影部分的面积为:S△ABC-S扇形BOE=$\frac{3\sqrt{3}}{2}$-$\frac{60π×{2}^{2}}{360}$=$\frac{3\sqrt{3}}{2}$-$\frac{2}{3}$π.
故选:C.
点评 此题主要考查了扇形的面积计算以及三角形面积求法等知识,根据已知得出△BOE和△ABE面积相等是解题关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
2.$-\frac{1}{8}$的倒数是( )
| A. | $\frac{1}{8}$ | B. | 8 | C. | -8 | D. | -1 |
3.若正比例函数的图象经过点(-1,2),(-m,4-2m),则m的值为( )
| A. | -1 | B. | -2 | C. | 2 | D. | 1 |
20.下列计算的结果正确的是( )
| A. | (-2a2)•3a=6a3 | B. | (-2x2)3=-8x6 | C. | a3+2a2=2a5 | D. | a3+a3=2a6 |
7. 如图,AD∥BC,AC平分∠BAD,∠1=51°,则∠B的大小为( )
如图,AD∥BC,AC平分∠BAD,∠1=51°,则∠B的大小为( )
 如图,AD∥BC,AC平分∠BAD,∠1=51°,则∠B的大小为( )
如图,AD∥BC,AC平分∠BAD,∠1=51°,则∠B的大小为( )| A. | 51° | B. | 60° | C. | 78° | D. | 88° |
4.下列运算能用平方差公式的是( )
| A. | (a+b)(-a+b) | B. | (m+n)(m+n) | C. | (-2x+y)(2x-y) | D. | -(p-q)(q-p) |
 如图所示,在△ABC中,∠C=90°,∠B=15°,AB的垂直平分线DE交BC于D点,垂足为E,BD=10,则AC的长为( )
如图所示,在△ABC中,∠C=90°,∠B=15°,AB的垂直平分线DE交BC于D点,垂足为E,BD=10,则AC的长为( )