题目内容
2.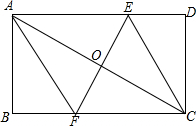 如图,把矩形ABCD沿EF对折,点A与点C恰好重合,已知AB=6cm,BC=8cm.
如图,把矩形ABCD沿EF对折,点A与点C恰好重合,已知AB=6cm,BC=8cm.(1)求证:四边形AFCE为菱形;
(2)求折痕EF的长.
分析 (1)平行四边形对角线互相垂直即为菱形;
(2)第二问中在直角三角形中,对角线BD是已知,可设BE的长为x,利用勾股定理求出BE,OE即可.
解答 证明:(1)∵把矩形ABCD沿EF对折,点A与点C恰好重合,
∴OA=OC,∠AOE=∠COF,
∵AD∥CB,
∴∠OAE=∠OF,
∴△AOE≌△COF,所以AE=CF,
∵AE∥CF,
∴四边形AFCE是平行四边形,
∵EF⊥AC,
∴四边形AFCE为菱形;
解:(2)由题意可得:EF垂直平分AC,
所以AE=CE,又OA=$\frac{1}{2}$AC=5,
设AE=EC=x,则DE=8-x,
在直角△CDE中,由勾股定理可得:x2=(8-x)2+62,解得x=$\frac{25}{4}$,
又在直角△OCE中,由勾股定理可得:OE=$\sqrt{C{E}^{2}-O{C}^{2}}$=$\frac{15}{4}$,
∵OE=OF,
∴EF=$\frac{15}{2}$.
点评 本题主要考查了折叠的性质、全等三角形的判定与性质、菱形的判定与性质以及勾股定理的综合应用,利用勾股定理列出方程是解决第2小题的关键.

练习册系列答案
相关题目
10. 已知,如上右图,动点P在函数y=$\frac{1}{2x}$(x>0)的图象上运动,PM⊥x轴于点M,PN⊥y轴于点N,线段PM、PN分别与直线AB:y=-x+1相交于点E,F,则AF•BE的值是( )
已知,如上右图,动点P在函数y=$\frac{1}{2x}$(x>0)的图象上运动,PM⊥x轴于点M,PN⊥y轴于点N,线段PM、PN分别与直线AB:y=-x+1相交于点E,F,则AF•BE的值是( )
 已知,如上右图,动点P在函数y=$\frac{1}{2x}$(x>0)的图象上运动,PM⊥x轴于点M,PN⊥y轴于点N,线段PM、PN分别与直线AB:y=-x+1相交于点E,F,则AF•BE的值是( )
已知,如上右图,动点P在函数y=$\frac{1}{2x}$(x>0)的图象上运动,PM⊥x轴于点M,PN⊥y轴于点N,线段PM、PN分别与直线AB:y=-x+1相交于点E,F,则AF•BE的值是( )| A. | 4 | B. | 2 | C. | 1 | D. | $\sqrt{2}$ |
7.下列命题中,假命题是( )
| A. | 等边三角形是等腰三角形 | B. | 如果ab=0,那么a=0且b=0 | ||
| C. | 如果a>0,b<0,那么ab<0 | D. | 全等三角形的面积相等 |
 如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数$y=\frac{m}{x}(m≠0)$的图象交于二四象限内的A、B 两点,与x轴交于C点,点B的坐标为(6,n),线段OA=5,E为x轴负半轴上一点,且sin∠AOE=$\frac{4}{5}$.
如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数$y=\frac{m}{x}(m≠0)$的图象交于二四象限内的A、B 两点,与x轴交于C点,点B的坐标为(6,n),线段OA=5,E为x轴负半轴上一点,且sin∠AOE=$\frac{4}{5}$. 如图△ABC中,点D是AC中点,点E在AB上,且∠B=90°,若DE=$\frac{1}{2}$AB,则命题:“DE是△ABC的中位线”是否正确?若正确,请说明理由;若不正确,请举例说明.
如图△ABC中,点D是AC中点,点E在AB上,且∠B=90°,若DE=$\frac{1}{2}$AB,则命题:“DE是△ABC的中位线”是否正确?若正确,请说明理由;若不正确,请举例说明.
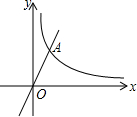 已知图中的曲线为反比例函数y=$\frac{k+2}{x}$(k为常数)的图象的一支.
已知图中的曲线为反比例函数y=$\frac{k+2}{x}$(k为常数)的图象的一支. 小明参加某网店的“翻牌抽奖”活动,如图,4张牌分别对应价值5,10,15,20(单位:元)的4件奖品.
小明参加某网店的“翻牌抽奖”活动,如图,4张牌分别对应价值5,10,15,20(单位:元)的4件奖品.