题目内容
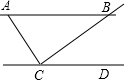如图，AB∥CD，AC⊥BC，图中与∠CAB互余的角有（ ）| A、1个 | B、2个 | C、3个 | D、0个 |
考点：平行线的性质,余角和补角,垂线
专题：
分析：根据平行线性质求出∠CBA=∠BCD，根据垂直定义求出∠ACB=90°，根据三角形内角和定理求出∠CAB+∠CBA=90°，根据余角定义判断即可．
解答：解：∵AB∥CD，
∴∠CBA=∠BCD，
∵AC⊥BC，
∴∠ACB=90°，
∴∠CAB+∠CBA=90°，
∴∠CAB+∠BCD=90°，
即图中与∠CAB互余的角有∠CBA和∠BCD两个．
故选B．
∴∠CBA=∠BCD，
∵AC⊥BC，
∴∠ACB=90°，
∴∠CAB+∠CBA=90°，
∴∠CAB+∠BCD=90°，
即图中与∠CAB互余的角有∠CBA和∠BCD两个．
故选B．
点评：本题考查了三角形的内角和定理，垂直，平行线的性质的应用，解此题的关键是推出∠CBA=∠BCD和∠CAB+∠CBA=90°，难度适中．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
下列从左到右的变形是因式分解的是（ ）
| A、（x+1）（x+3）=x2+4x+3 |
| B、x2-2x+1=x（x-2）+1 |
| C、a2-9=（a+3）（a-3） |
| D、2x（a+b）=2ax+2bx |