题目内容
已知|x-1|+(y+3)2=0,且(a+1)x+1=y,求a的值.
考点:解一元一次方程,非负数的性质:绝对值,非负数的性质:偶次方
专题:计算题
分析:利用非负数的性质求出x与y的值,代入方程计算即可求出a的值.
解答:解:∵|x-1|+(y+3)2=0,
∴x-1=0,y+3=0,
解得:x=1,y=-3,
代入方程得:a+1+1=-3,
解得:a=-5.
∴x-1=0,y+3=0,
解得:x=1,y=-3,
代入方程得:a+1+1=-3,
解得:a=-5.
点评:此题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,把未知数系数化为1,求出解,熟练掌握非负数的性质是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列各式中计算正确的是( )
A、
| ||||||
B、
| ||||||
C、(-
| ||||||
D、
|
若最简二次根式
与
是同类二次根式,则a的值为( )
| 1+a |
| 2 |
A、-
| ||
B、
| ||
| C、1 | ||
| D、-1 |
 如图,平行四边形ABCD中,P是形内任意一点,△ABP,△BCP,△CDP,△ADP的面积分别为S1,S2,S3,S4,则一定成立的是( )
如图,平行四边形ABCD中,P是形内任意一点,△ABP,△BCP,△CDP,△ADP的面积分别为S1,S2,S3,S4,则一定成立的是( )| A、S1+S2>S3+S4 |
| B、S1+S2=S3+S4 |
| C、S1+S2<S3+S4 |
| D、S1+S3=S2+S4 |
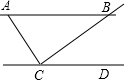 如图,AB∥CD,AC⊥BC,图中与∠CAB互余的角有( )
如图,AB∥CD,AC⊥BC,图中与∠CAB互余的角有( )| A、1个 | B、2个 | C、3个 | D、0个 |
 “中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70千米/小时,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面对车速检测仪正前方30米处,过了3秒后,测得小汽车与车速检测仪间距离为50米,这辆小汽车超速了吗?
“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70千米/小时,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面对车速检测仪正前方30米处,过了3秒后,测得小汽车与车速检测仪间距离为50米,这辆小汽车超速了吗? 请画出图中任一点关于另外两点所在直线为对称轴的对称点.
请画出图中任一点关于另外两点所在直线为对称轴的对称点.