题目内容
在直角三角形中一个锐角是30°，则斜边上的中线把直角分别两部分，它的度数分别是 ， ．
考点：直角三角形斜边上的中线
专题：
分析：作出图形，根据直角三角形斜边上的中线等于斜边的一半可得CD=AD=BD，再根据等边对等角求出∠ACD=∠A，然后求出∠BCD即可．
解答：
解：如图，∵CD是Rt△ABC斜边上的中线，
∴CD=AD=BD，
∴∠ACD=∠A=30°，
∴∠BCD=90°-30°=60°．
故答案为：30°，60°．
解：如图，∵CD是Rt△ABC斜边上的中线，∴CD=AD=BD，
∴∠ACD=∠A=30°，
∴∠BCD=90°-30°=60°．
故答案为：30°，60°．
点评：本题考查了直角三角形斜边上的中线等于斜边的一半的性质，等腰三角形的性质，熟记性质是解题的关键，作出图形更形象直观．
练习册系列答案
相关题目
在△ABC中，∠A=90°，BD平分∠ABC，AD=3cm，BC=10cm，求△DBC的面积．已知抛物线经过点（0，4），（1，-1），（2，4），那么它的对称轴是直线（ ）
| A、x=-1 | B、x=1 |
| C、x=3 | D、x=-3 |
下列各式中计算正确的是（ ）
A、
| ||||||
B、
| ||||||
C、(-
| ||||||
D、
|
在下列式子：①8x；②-8x；③64x4；④-64x4中，选择一个与16x2+1相加后，成为一个完全平方式，则符合条件的式子有（ ）
| A、4个 | B、3个 | C、2个 | D、1个 |
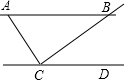如图，AB∥CD，AC⊥BC，图中与∠CAB互余的角有（ ）| A、1个 | B、2个 | C、3个 | D、0个 |