题目内容
5. 如图,在△ABC和△DEF中,点B,F,C,E在同一直线上,BF=CE,AC=DF,AC∥DF. 求证:
如图,在△ABC和△DEF中,点B,F,C,E在同一直线上,BF=CE,AC=DF,AC∥DF. 求证:(1)△ABC≌△DEF;
(2)AB∥DE.
分析 (1)依据平行的性质可证明∠ACB=∠DFE,依据等式的性质可证明BC=EF,最后依据SAS进行证明即可;
(2)依据全等三角形的性质可得到∠B=∠E,最后依据内错角相等两直线平行进行证明即可.
解答 证明:(1)∵AC∥DF,
∴∠ACB=∠DFE.
∵BF=CE,
∴BF+FC=CE+FC,即BC=EF.
在△ABC和△DEF中$\left\{\begin{array}{l}BC=EF\\∠ACB=∠DFE\\ AC=DF\end{array}\right.$
∴△ABC≌△DEF(SAS).
(2)解:∵△ABC≌△DEF,
∴∠B=∠E.
∴AB∥DE.
点评 本题主要考查的是全等三角形的性质和判定,解答本题主要应用了全等三角形的性质和判定、平行线的性质和判定,熟练掌握全等三角形的判定定理是解题的关键.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案
相关题目
15.去括号-a-(b-2)=( )
| A. | -a-b-2 | B. | a+b-2 | C. | -a-b+2 | D. | -a+b-2 |
16.下列计算结果正确的是( )
| A. | (-3)2=6 | B. | (-1)2017=-1 | C. | -2+3=-5 | D. | -|-3|=3 |
13.若一个多边形的每一个外角都是45°,则这个多边形是( )
| A. | 六边形 | B. | 七边形 | C. | 八边形 | D. | 九边形 |
3. 如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3=( )
如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3=( )
 如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3=( )
如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3=( )| A. | 90° | B. | 135° | C. | 150° | D. | 180° |
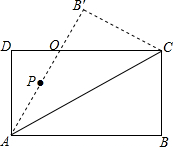 如图,在矩形ABCD中,∠CAB=30°,BC=4$\sqrt{3}$cm,将△ABC沿AC边翻折,使点B到点B′,AB′与DC相交于点O.
如图,在矩形ABCD中,∠CAB=30°,BC=4$\sqrt{3}$cm,将△ABC沿AC边翻折,使点B到点B′,AB′与DC相交于点O.