题目内容
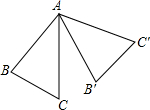 如图,将△ABC绕着顶点A逆时针旋转了70°后,得到△AB′C′,若∠B+∠C=130°,则∠CAB′的度数为( )
如图,将△ABC绕着顶点A逆时针旋转了70°后,得到△AB′C′,若∠B+∠C=130°,则∠CAB′的度数为( )| A、20° | B、50° |
| C、60° | D、70° |
考点:旋转的性质
专题:
分析:如图,由三角形内角和定理求出∠BAC;借助∠BAB′=70°,即可解决问题.
解答: 解:∵∠B+∠C=130°,
解:∵∠B+∠C=130°,
∴∠BAC=180°-130°=50°;
由题意得:∠BAB′=70°,
∴∠CAB′=70°-50°=20°,
故选A.
 解:∵∠B+∠C=130°,
解:∵∠B+∠C=130°,∴∠BAC=180°-130°=50°;
由题意得:∠BAB′=70°,
∴∠CAB′=70°-50°=20°,
故选A.
点评:该题主要考查了旋转变换的性质、三角形的内角和定理及其应用问题;解题的关键是灵活运用旋转变换的质,三角形的内角和定理等来分析、判断、解答.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
 小明玩数学游戏,利用四张完全相同的小长方形纸板测量一张正方形纸板的边长,将它们如图放置,测量的数据如图,则这张正方形纸板的边长为( )
小明玩数学游戏,利用四张完全相同的小长方形纸板测量一张正方形纸板的边长,将它们如图放置,测量的数据如图,则这张正方形纸板的边长为( )| A、60cm | B、70cm |
| C、80cm | D、90cm |
 如图,C,D是线段AB上两点,若CB=4cm,DB=7cm,且D是AC的中点,则AC的长等于( )
如图,C,D是线段AB上两点,若CB=4cm,DB=7cm,且D是AC的中点,则AC的长等于( )| A、3cm | B、6cm |
| C、11cm | D、14cm |
关于函数y=x2-2x-3的叙述:
①当x>1时,y的值随x的增大而增大
②y的最小值是-3
③函数图象与x轴交点的横坐标是方程x2-2x-3=0的根
④函数图象与y轴交点的坐标是(0,-3)
⑤函数图象经过第一、二、三、四象限
其中正确的有( )
①当x>1时,y的值随x的增大而增大
②y的最小值是-3
③函数图象与x轴交点的横坐标是方程x2-2x-3=0的根
④函数图象与y轴交点的坐标是(0,-3)
⑤函数图象经过第一、二、三、四象限
其中正确的有( )
| A、2个 | B、3个 | C、4个 | D、5个 |
下列说法错误的是( )


| A、图①中直线l经过点A |
| B、图②中直线a,b相交于点A |
| C、图③中点C在线段AB上 |
| D、图④中射线CD与AB有公共点 |
请你运用学过的函数知识,判断下列哪一个图象可能是函数y=x3的图象( )
A、 |
B、 |
C、 |
D、 |
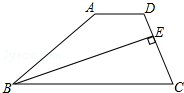 如图,在梯形ABCD中,AD∥BC,BE平分∠ABC交CD于E,且BE⊥CD,CE:ED=2:1.如果△BEC的面积为2,那么四边形ABED的面积是( )
如图,在梯形ABCD中,AD∥BC,BE平分∠ABC交CD于E,且BE⊥CD,CE:ED=2:1.如果△BEC的面积为2,那么四边形ABED的面积是( )