Question

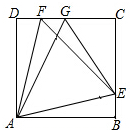
2．已知，在四边形ABCD中，点E、F分别在边BC、DC上，连接AF、EF．
（1）如图1，若四边形ABCD为正方形，且∠EAF=45°，求证：EF=BE+DF；
（2）如图2，若四边形ABCD中，AB=AD，∠B+∠D=180°，∠EAF=$\frac{1}{2}$∠BAD，试问（1）中的结论还成立吗？如果成立，请给出证明；如果不成立，请说明理由．

Answer 1

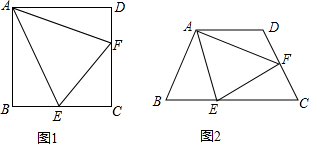
分析 （1）延长CB到G，使BG=FD，根据已知条件容易证明△ABG≌△ADF，由此可以推出∠BAG=∠DAF，AG=AF，而∠EAF=$\frac{1}{2}$∠BAD，所以得到∠DAF+∠BAE=∠EAF，进一步得到∠EAF=∠GAE，现在可以证明△AEF≌△AEG，然后根据全等三角形的性质就可以证明结论成立；
（2）把△ADF绕点A顺时针旋转∠DAB的度数得到△ABG，如图，根据旋转的性质得到∠ADF=∠ABG，∠GAF=∠BAD，AG=AF，BG=DF，再证明点G在CB的延长线上，
即GE=BG+BE，然后证明△AEG≌△AEF，得到EF=GE，所以EF=BE+BG=BE+DF．

解答 解：（1）如图①，延长CB到G，使BG=FD，

∵∠ABG=∠D=90°，AB=AD，
∴△ABG≌△ADF，
∴∠BAG=∠DAF，AG=AF，
∵∠EAF=$\frac{1}{2}$∠BAD，
∴∠DAF+∠BAE=∠EAF，
∴∠EAF=∠GAE，
在△AEG和△AEF中，
$\left\{\begin{array}{l}{AG=AF}\\{∠GAE=∠FAE}\\{AE=AE}\end{array}\right.$，
∴△AEF≌△AEG，
∴EF=EG=EB+BG=EB+DF；

（2）（1）中的结论还成立，理由如下：
把△ADF绕点A顺时针旋转∠DAB的度数得到△ABG，如图②，②
∴∠ADF=∠ABG，∠GAF=∠BAD，AG=AF，BG=DF，
∵∠ABC+∠ADC=180°，
∴∠ABC+∠ABG=180°，
∴点G在CB的延长线上，
∴GE=BG+BE，
∵∠EAF=$\frac{1}{2}$∠BAD，
∴∠EAF=$\frac{1}{2}$∠GAE，
∴∠EAF=∠GAE，
在△AEG和△AEF中，
$\left\{\begin{array}{l}{AG=AF}\\{∠GAE=∠FAE}\\{AE=AE}\end{array}\right.$，
∴△AEG≌△AEF（SAS），
∴EF=GE，
∴EF=BE+BG=BE+DF．

点评 本题考查了正方形的性质，全等三角形的判定与性质，旋转变换的性质，利用旋转变换构造出全等三角形是解题的关键，也是本题的难点．