题目内容
19. 如图,⊙O的弦AB⊥CD,AD=2,BC=3,求⊙O的直径长.
如图,⊙O的弦AB⊥CD,AD=2,BC=3,求⊙O的直径长.
分析 连接AC,由AB⊥CD,得到∠CAB+∠ACD=90°,于是得到$\widehat{BC}+\widehat{AD}$=半圆弧,在圆周上截取$\widehat{BE}$=$\widehat{AD,}$连接CE,得到BE=AD=2,等量代换得到$\widehat{BC}+\widehat{BE}$=半圆弧,推出CE是⊙O的直径,根据圆周角定理得到∠CBE=90°,根据勾股定理即可得到结论.
解答  解:连接AC,
解:连接AC,
∵AB⊥CD,
∴∠CAB+∠ACD=90°,
∴$\widehat{BC}+\widehat{AD}$=半圆弧,
在圆周上截取$\widehat{BE}$=$\widehat{AD,}$连接CE,
∴BE=AD=2,
∴$\widehat{BC}+\widehat{BE}$=半圆弧,
∴CE是⊙O的直径,
∴∠CBE=90°,
∴CE=$\sqrt{B{C}^{2}+B{E}^{2}}$=$\sqrt{13}$,
即⊙O的直径长为$\sqrt{13}$.
点评 此题考查了圆周角定理、相似三角形的判定与性质以及勾股定理,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
9.用科学记数法表示:2015000是( )
| A. | 2.015×106 | B. | 2.015×107 | C. | 0.2015×107 | D. | 2015×103 |
4.合肥市轨道交通1号线隧道工程于今年10月实现全线钻通,项目总投资159.91亿元.“159.91亿”用科学记数法表示正确的是( )
| A. | 159.91×108 | B. | 1.5991×108 | C. | 1.5991×109 | D. | 1.5991×1010 |
8.下列说法正确的是( )
| A. | $-\frac{1}{4}$xy3是整式 | B. | x3y2系数为0 | C. | $\frac{1}{a}$是单项式 | D. | 3不是单项式 |
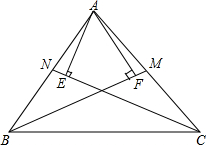 如图,已知AB=AC,BM,CN分别是AC,AB边上的中线,AE⊥CN、AF⊥BM,垂足分别为E,F,求证:AE=AF.
如图,已知AB=AC,BM,CN分别是AC,AB边上的中线,AE⊥CN、AF⊥BM,垂足分别为E,F,求证:AE=AF.