题目内容
11. 如图,在⊙O中,直径AB交弦CD于点G,CG=DG,⊙O的切线BE与DO的延长线相交于点E,DO的延长线交⊙O于点F,连接BD,BF.
如图,在⊙O中,直径AB交弦CD于点G,CG=DG,⊙O的切线BE与DO的延长线相交于点E,DO的延长线交⊙O于点F,连接BD,BF.(1)求证:∠CDE=∠E;
(2)若OD=4,EF=1,求BF的长.
分析 (1)由在⊙O中,直径AB交弦CD于点G,CG=DG,根据垂径定理即可得AB⊥CD,又由BE是⊙O的切线,易证得CD∥BE,即可证得结论;
(2)易证得△ODG∽△OEB,然后由相似三角形的对应边成比例,求得OG的长,由勾股定理即可求得DG的长,作FH⊥AB于点H.则CD∥FH,在直角△BHF中利用勾股定理即可求得BF的长.
解答 (1)证明:∵在⊙O中,直径AB交弦CD于点G,CG=DG,
∴AB⊥CD,
∵BE是⊙O的切线,
∴AB⊥BE,
∴CD∥BE,
∴∠CDE=∠E;
(2)解:∵∠CDE=∠E,∠DOG=∠BOE,
∴△ODG∽△OEB,
∴$\frac{OG}{OB}$=$\frac{OD}{OE}$,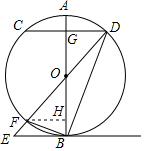
∵OD=4,EF=1,
∴OB=OF=OD=4,
∴OE=OF+EF=5,
∴$\frac{OG}{4}$=$\frac{4}{5}$,
∴OG=$\frac{16}{5}$,
∴DG=$\sqrt{O{D}^{2}-O{G}^{2}}$=$\frac{12}{5}$,
作FH⊥AB于点H.则CD∥FH,
又∵OF=OD,
∴FH=DG=$\frac{12}{5}$,OH=OG=$\frac{16}{5}$,
∴BH=OB-OH=4-$\frac{16}{5}$=$\frac{4}{5}$,
∴Rt△BHF中,BF=$\sqrt{B{H}^{2}+F{H}^{2}}$=$\sqrt{(\frac{4}{5})^{2}+(\frac{12}{5})^{2}}$=$\frac{4\sqrt{10}}{5}$.
点评 此题考查了切线的性质、垂径定理以及相似三角形的判定与性质.注意证得△ODG∽△OEB是解此题的关键.

练习册系列答案
相关题目
2.下列图形既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
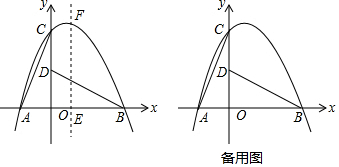

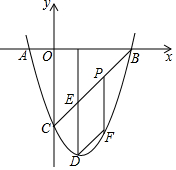 如图,抛物线y=x2+bx+c与x轴相交于A、B两点,点B的坐标为(3,0),与y轴相交于点C(0,-3),顶点为D.
如图,抛物线y=x2+bx+c与x轴相交于A、B两点,点B的坐标为(3,0),与y轴相交于点C(0,-3),顶点为D. 正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示的方式放置,点A1,A2,A3…和点C1,C2,C3…分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2),则B2017的坐标是(22017-1,22016).
正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示的方式放置,点A1,A2,A3…和点C1,C2,C3…分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2),则B2017的坐标是(22017-1,22016). 如图,已知A(1,6)B(n,-2)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点,直线与y轴交于C点.
如图,已知A(1,6)B(n,-2)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点,直线与y轴交于C点.