题目内容
16.若f(x)=2x-1(如f(-2)=2×(-2)-1),f(3)=2×(3)-1,求$\frac{f(1)+f(2)+…+f(2009)}{2009}$的值.分析 根据自变量与函数值的对应关系,可得有理数的加法,根据自然数的和,可得答案.
解答 解:原式=$\frac{2×1-1+2×2-1+2×3-1+…+2×2009-1}{2009}$
=$\frac{2×(1+2+3+…2009)-2009}{2009}$
=$\frac{2009(2009+1)-2009}{2009}$
=$\frac{200{9}^{2}}{2009}$
=2009.
点评 本题考查了函数值,利用自然数的和1+2+3+…n=$\frac{n(1+n)}{2}$是解题关键.

练习册系列答案
相关题目
4.设a>0,则(5b$\sqrt{\frac{a}{b}}$+$\frac{1}{a}$$\sqrt{{a}^{3}b}$)-(2a$\sqrt{\frac{b}{a}}$+$\sqrt{25ab}$)的值一定是( )
| A. | 正数 | B. | 负数 | C. | 0 | D. | 1 |
1. 如图,直线AB、CD交于点O,OE平分∠AOD,∠AOE=65°,则∠AOC=( )
如图,直线AB、CD交于点O,OE平分∠AOD,∠AOE=65°,则∠AOC=( )
 如图,直线AB、CD交于点O,OE平分∠AOD,∠AOE=65°,则∠AOC=( )
如图,直线AB、CD交于点O,OE平分∠AOD,∠AOE=65°,则∠AOC=( )| A. | 20° | B. | 40° | C. | 50° | D. | 80° |
 如图,DC∥EF∥GH∥AB,AB=12,CD=6,DE:EG:GA=3:4:5.求EF和GH的长.
如图,DC∥EF∥GH∥AB,AB=12,CD=6,DE:EG:GA=3:4:5.求EF和GH的长. 如图,已知△ABC中,BC>AC,求证:∠A>∠B.
如图,已知△ABC中,BC>AC,求证:∠A>∠B.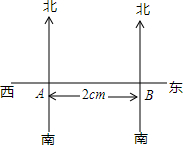 如图,某轮船上午8时在A处测得灯塔S在北偏东60°方向上,当轮船继续向东行驶,中午12时到达B处,在B处测得灯塔S在北偏西30°的方向上,已知轮船行驶的速度为20km/h.
如图,某轮船上午8时在A处测得灯塔S在北偏东60°方向上,当轮船继续向东行驶,中午12时到达B处,在B处测得灯塔S在北偏西30°的方向上,已知轮船行驶的速度为20km/h. 在Rt△ABC中,∠C=90°,∠A<∠B,AM=BM=CM,沿CM将三角形AMC翻折,点A落在点D,CD⊥AB,则∠A=30度.
在Rt△ABC中,∠C=90°,∠A<∠B,AM=BM=CM,沿CM将三角形AMC翻折,点A落在点D,CD⊥AB,则∠A=30度.