题目内容
10.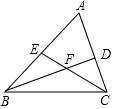 如图,在△ABC中,∠A=60°,∠ABC与∠ACB的平分线分别交AC,AB于点D,E.BD,CE相交于点F,现给出以下四个结论:①∠BFE=60°;②FE=FD;③AE=AD;④BD=BC.其中正确的是①②(把所有正确结论的序号都填在横线上)
如图,在△ABC中,∠A=60°,∠ABC与∠ACB的平分线分别交AC,AB于点D,E.BD,CE相交于点F,现给出以下四个结论:①∠BFE=60°;②FE=FD;③AE=AD;④BD=BC.其中正确的是①②(把所有正确结论的序号都填在横线上)
分析 ①正确.只要求出∠BFC即可解决问题;
②正确.在BC上截取BG=BE,连接FG.只要证明△EBF≌△GBF(SAS),△FDC≌△FGC(ASA)即可解决问题;
③④错误,假设成立,推出矛盾即可.
解答 解:如图,∵∠A=60°,BD、CE分别是∠ABC和∠BCA的平分线,
∴∠FBC+∠FCB=$\frac{1}{2}$(∠ABC+∠ACB)=60°
∴∠BFC=180°-60°=120°,
∴∠BFE=180°-∠BFC=60°故①正确,
在BC上截取BG=BE,连接FG.
∵BD是∠BAC的平分线,
∴∠EBF=∠GBF,
在△EAF和△GAF中
∵$\left\{\begin{array}{l}{BE=BG}\\{∠EBF=∠GBF}\\{BF=BF}\end{array}\right.$,
∴△EBF≌△GBF(SAS),
∴FE=FG,∠EFB=∠GFB=60°,
∴∠GFC=180°-60°-60°=60°,
又∵∠DFC=∠EFB=60°,
∴∠DFC=∠GFC,
在△FDC和△FGC中
∵$\left\{\begin{array}{l}{∠DFC=∠GFC}\\{FC=FC}\\{∠FCD=∠FCG}\end{array}\right.$,
∴△FDC≌△FGC(ASA),
∴FD=FG,
∴FE=FD,故②正确,
AE不一定等于AD,若AE=AD则△ABC是等边三角形,显然不可能,故③错误,
BD不一定等于BC,若BD=BC,可以推出∠ABC=40°,显然不可能,故④错误,
故答案为①②.
点评 本题考查等边三角形的性质、全等三角形的判定和性质.解题的关键是学会添加常用辅助线面构造全等三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
18.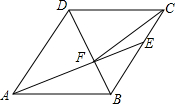 如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,若CE=2,连接CF.以下结论:①∠BAF=∠BCF;②点E到AB的距离是2$\sqrt{3}$;③S△CDF:S△BEF=9:4;④tan∠DCF=$\frac{3}{7}$.其中正确的有( )
如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,若CE=2,连接CF.以下结论:①∠BAF=∠BCF;②点E到AB的距离是2$\sqrt{3}$;③S△CDF:S△BEF=9:4;④tan∠DCF=$\frac{3}{7}$.其中正确的有( )
 如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,若CE=2,连接CF.以下结论:①∠BAF=∠BCF;②点E到AB的距离是2$\sqrt{3}$;③S△CDF:S△BEF=9:4;④tan∠DCF=$\frac{3}{7}$.其中正确的有( )
如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,若CE=2,连接CF.以下结论:①∠BAF=∠BCF;②点E到AB的距离是2$\sqrt{3}$;③S△CDF:S△BEF=9:4;④tan∠DCF=$\frac{3}{7}$.其中正确的有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
5.在下列几个几何体中,主视图与俯视图都是圆的是( )
| A. | 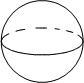 | B. | 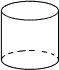 | C. |  | D. |  |
15.下列图形中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
19.下列说法中,正确的是( )
| A. | 任何数都有两个平方根 | B. | 9的平方根只有3 | ||
| C. | (-2)3的立方根为2 | D. | 0.04的算术平方根为0.2 |

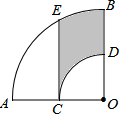 如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交弧AB于点E,以点O为圆心,OC的长为半径作弧CD交OB于点D,若OA=4,则阴影部分的面积为$\frac{1}{3}$π+2$\sqrt{3}$.
如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交弧AB于点E,以点O为圆心,OC的长为半径作弧CD交OB于点D,若OA=4,则阴影部分的面积为$\frac{1}{3}$π+2$\sqrt{3}$.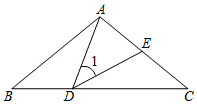 如图,△ABC中,AB=AC=5cm,∠BAC=100°,点D在线段BC上运动(不与点B、C重合),连接AD,作∠1=∠C,DE交线段AC于点E.
如图,△ABC中,AB=AC=5cm,∠BAC=100°,点D在线段BC上运动(不与点B、C重合),连接AD,作∠1=∠C,DE交线段AC于点E.