题目内容
17.已知A(-1,y1)、B(2,y2)、C(-$\sqrt{2}$,y3)在函数y=-2(x-1)2+1的图象上,则y1、y2、y3的大小关系是y3<y1<y2.(用“<”连接)
分析 先求得函数y═-2(x-1)2+1的对称轴为x=1,再判断点(2,y2)的对称点的坐标为(0,y4),从而判断出y2=y4.
解答 解:∵对称轴为x=1,
∴点(2,y2)的对称点的横坐标为0,即对称点坐标为(0,y4),
y2=y4.
-$\sqrt{2}$<-1<0,由a=-2,对称轴的左侧y随x的增大而增大,得
y3<y1<y4.
即y3<y1<y2,
故答案为:y3<y1<y2.
点评 本题考查了二次函数图象上点的坐标特征,本题的关键是:(1)找到二次函数的对称轴;(2)根据对称性将两个点移到对称轴同侧比较.

练习册系列答案
相关题目
6.(-3a2)•(2ab2)•(-b)2 的计算结果是( )
| A. | -6a2b3 | B. | 6a3b3 | C. | -6 a3b4 | D. | 6a3b4 |
 如图,边长为6的正方形ABCD中,E是AB边上的一点,且AE=2BE,已知F是CE的中点,将△CDF沿着DF翻折至△GDF,连接BG,则S四边形BFDG=$\frac{228}{17}$.
如图,边长为6的正方形ABCD中,E是AB边上的一点,且AE=2BE,已知F是CE的中点,将△CDF沿着DF翻折至△GDF,连接BG,则S四边形BFDG=$\frac{228}{17}$. 如图,已知二次函数y1=ax2+bx+c(a≠0)与一次函数y2=kx+m(k≠0)的图象相交于点A(-2,4),B(9,2),那么能使y2>y1成立的x的取值范围是-2<x<9.
如图,已知二次函数y1=ax2+bx+c(a≠0)与一次函数y2=kx+m(k≠0)的图象相交于点A(-2,4),B(9,2),那么能使y2>y1成立的x的取值范围是-2<x<9. 如图,I是△ABC的内心,AI的延长线与△ABC的外接圆相交于点D,与BC交于点E,连接BI、CI、BD、DC.下列说法中正确的有( )
如图,I是△ABC的内心,AI的延长线与△ABC的外接圆相交于点D,与BC交于点E,连接BI、CI、BD、DC.下列说法中正确的有( )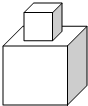 如图所示的某种玩具是由两个正方体用胶水黏合而成的,它们的棱长分别为1dm和2dm,为了美观,现要在其表面喷涂油漆,如果喷涂1dm2需用油漆4g,那么喷涂这个玩具共需油漆112g.
如图所示的某种玩具是由两个正方体用胶水黏合而成的,它们的棱长分别为1dm和2dm,为了美观,现要在其表面喷涂油漆,如果喷涂1dm2需用油漆4g,那么喷涂这个玩具共需油漆112g.