题目内容
16. 如图,已知AB∥CD,O是∠BAC与∠ACD的平分线的交点.OE⊥AC于E,OE=2,则点O到AB与CD的距离之和为4.
如图,已知AB∥CD,O是∠BAC与∠ACD的平分线的交点.OE⊥AC于E,OE=2,则点O到AB与CD的距离之和为4.
分析 过点O作MN,MN⊥AB于M,求出MN⊥CD,则MN的长度是AB和CD之间的距离;然后根据角平分线的性质,分别求出OM、ON的长度是多少,再把它们求和即可.
解答 解:如图,过点O作MN,MN⊥AB于M,交CD于N,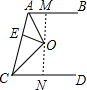
∵AB∥CD,
∴MN⊥CD,
∵AO是∠BAC的平分线,OM⊥AB,OE⊥AC,OE=2,
∴OM=OE=2,
∵CO是∠ACD的平分线,OE⊥AC,ON⊥CD,
∴ON=OE=2,
∴MN=OM+ON=4,
即AB与CD之间的距离是4.
故答案为:4.
点评 此题主要考查了角平分线的性质和平行线之间的距离的应用,要熟练掌握,解答此题的关键是要明确:①角的平分线上的点到角的两边的距离相等,②从一条平行线上的任意一点到另一条直线作垂线,垂线段的长度叫两条平行线之间的距离,③平行线间的距离处处相等.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
6.设两数为a,b,那么代数式$\frac{5(a-b)^{2}}{2}$表示( )
| A. | a与b的平方差的5倍除以2 | B. | a与b的差的平方的5倍除以2 | ||
| C. | a的5倍与b的差的平方的一半 | D. | a的5倍与b的平方差的一半 |
1.下列说法:
①-$\sqrt{17}$是17的平方根;
②$\frac{1}{27}$的立方根是±$\frac{1}{3}$;
③-81没有立方根;
④互为相反数的两个数的立方根也互为相反数,
错误的有( )
①-$\sqrt{17}$是17的平方根;
②$\frac{1}{27}$的立方根是±$\frac{1}{3}$;
③-81没有立方根;
④互为相反数的两个数的立方根也互为相反数,
错误的有( )
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
8.下列4组线段中,不能组成直角三角形的是( )
| A. | a=3,b=4,c=5 | B. | a=2,b=3,c=4 | C. | a=5,b=12,c=13 | D. | a=8,b=15,c=17 |
6.圆柱的侧面展开图( )
| A. | 是平行四边形 | B. | 一定是正方形 | C. | 可能是菱形 | D. | 必是矩形 |
 如图,D,E分别为△ABC的AC,BC边的中点,将此三角形沿DE折叠,使点C落在AB边上的点P处.若∠CDE=50°,则∠APD等于50°.
如图,D,E分别为△ABC的AC,BC边的中点,将此三角形沿DE折叠,使点C落在AB边上的点P处.若∠CDE=50°,则∠APD等于50°.