题目内容
如图所示，AD，BE是钝角△ABC的边BC，AC上的高，求证：| AD |
| BE |
| AC |
| BC |
考点：相似三角形的判定与性质
专题：证明题
分析：由AD，BE是钝角△ABC的边BC，AC上的高，可得∠D=∠E=90°，又由∠ACD=∠BCE，即可证得△ACD∽△BCE，然后由相似三角形的对应边成比例，证得结论．
解答：证明：∵AD，BE是钝角△ABC的边BC，AC上的高，
∴∠D=∠E=90°，
∵∠ACD=∠BCE，
∴△ACD∽△BCE，
∴
=
．
∴∠D=∠E=90°，
∵∠ACD=∠BCE，
∴△ACD∽△BCE，
∴
| AD |
| BE |
| AC |
| BC |
点评：此题考查了相似三角形的判定与性质．此题比较简单，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
如图，在四边形ABCD中，AD∥BC，AB=CD=2，BC=5，∠BAD的平分线交BC于点E，且AE∥CD，则四边形ABCD的面积为下列调查用全面调查合适的是（ ）
| A、调查我省中小学学习负担是否过重 |
| B、调查我省中小学课外资料花费情况 |
| C、调查某班同学的身高情况 |
| D、调查某种奶粉的合格率 |
已知：如图，D、E、F分别是BC、CA、AB上的点，DE∥AB，DF∥CA．求证：∠EDF=∠A（写出证明过程，并注明各步理由）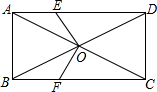
如图，在矩形ABCD中，对角线AC，BD相交于点O，点E，F分别在边AD，BC上，且DE=CF，连接OE，OF．求证：OE=OF．