题目内容
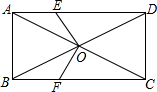 如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别在边AD,BC上,且DE=CF,连接OE,OF.求证:OE=OF.
如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别在边AD,BC上,且DE=CF,连接OE,OF.求证:OE=OF.考点:全等三角形的判定与性质,矩形的性质
专题:证明题
分析:欲证明OE=OF,只需证得△ODE≌△OCF即可.
解答: 证明:如图,∵四边形ABCD是矩形,
证明:如图,∵四边形ABCD是矩形,
∴∠ADC=∠BCD=90°,
AC=BD,OD=
BD,OC=
AC,
∴OD=OC,
∴∠ODC=∠OCD,
∴∠ADC-∠ODC=∠BCD-∠OCD,
即∠EDO=∠FCO,
在△ODE与△OCF中,
,
∴△ODE≌△OCF(SAS),
∴OE=OF.
 证明:如图,∵四边形ABCD是矩形,
证明:如图,∵四边形ABCD是矩形,∴∠ADC=∠BCD=90°,
AC=BD,OD=
| 1 |
| 2 |
| 1 |
| 2 |
∴OD=OC,
∴∠ODC=∠OCD,
∴∠ADC-∠ODC=∠BCD-∠OCD,
即∠EDO=∠FCO,
在△ODE与△OCF中,
|
∴△ODE≌△OCF(SAS),
∴OE=OF.
点评:本题考查了全等三角形的判定与性质,矩形的性质.全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.

练习册系列答案
相关题目
把多项式(m+1)(m-1)+(m+1)提取公因式m+1后,余下的部分是( )
| A、m+1 | B、m-1 |
| C、m | D、2 m+1 |
平面直角坐标系中有A(-2,-1),B(-4,3),C(0,0),则三角形ABC的面积为( )
| A、5 | B、6 | C、8 | D、3 |
 如图所示,AD,BE是钝角△ABC的边BC,AC上的高,求证:
如图所示,AD,BE是钝角△ABC的边BC,AC上的高,求证: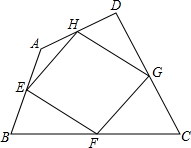 如图,我们把依次连接任意四边形ABCD各边中点所得四边形EFGH叫中点四边形.
如图,我们把依次连接任意四边形ABCD各边中点所得四边形EFGH叫中点四边形.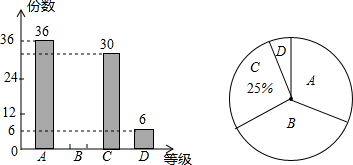
 将某雷达测速区监测到的一组汽车的时速数据整理,得到其频数分布表(未完成):
将某雷达测速区监测到的一组汽车的时速数据整理,得到其频数分布表(未完成):