题目内容
 (1)在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AC,交AB于E,若AB=5,求线段DE的长.
(1)在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AC,交AB于E,若AB=5,求线段DE的长.(2)已知x2-4x+1=0,求
| 2(x-1) |
| x-4 |
| x+6 |
| x |
考点:等腰三角形的判定与性质,分式的化简求值,平行线的性质,直角三角形斜边上的中线
专题:
分析:(1)求出∠CAD=∠BAD=∠EDA,推出AE=DE,求出∠ABD=∠EDB,推出BE=DE,求出AE=BE,根据直角三角形斜边上中线性质求出即可.
(2)化简以后,用整体思想代入即可得到答案.
(2)化简以后,用整体思想代入即可得到答案.
解答:解:(1)∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵DE∥AC,
∴∠CAD=∠ADE,
∴∠BAD=∠ADE,
∴AE=DE,
∵AD⊥DB,
∴∠ADB=90°,
∴∠EAD+∠ABD=90°,∠ADE+∠BDE=∠ADB=90°,
∴∠ABD=∠BDE,
∴DE=BE,
∵AB=5,
∴DE=BE=AE=
AB=2.5.
(2)原式=
=
∵x2-4x+1=0,∴x2-4x=-1,
原式=
=-23
∴∠BAD=∠CAD,
∵DE∥AC,
∴∠CAD=∠ADE,
∴∠BAD=∠ADE,
∴AE=DE,
∵AD⊥DB,
∴∠ADB=90°,
∴∠EAD+∠ABD=90°,∠ADE+∠BDE=∠ADB=90°,
∴∠ABD=∠BDE,
∴DE=BE,
∵AB=5,
∴DE=BE=AE=
| 1 |
| 2 |
(2)原式=
| 2x(x-1)-(x-4)(x+6) |
| x(x-4) |
=
| x2-4x+24 |
| x2-4x |
∵x2-4x+1=0,∴x2-4x=-1,
原式=
| -1+24 |
| -1 |
点评:本题考查了平行线的性质,等腰三角形的性质和判定,直角三角形斜边上中线性质的应用,关键是求出DE=BE=AE.学会用整体思想解答有关问题是我们学习的关键.

练习册系列答案
相关题目
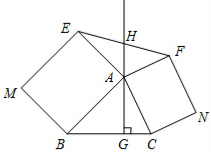 如图,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF,射线GA交EF于点H.若AB=kAE,AC=kAF,试探究HE与HF之间的数量关系,并说明理由.
如图,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF,射线GA交EF于点H.若AB=kAE,AC=kAF,试探究HE与HF之间的数量关系,并说明理由.