题目内容
古希腊数学家把数1,3,6,10,15,21…叫做三角形数,它有一定的规律性,若把第一个三角形数记为a1,第二个三角形数记为a2,…,第n个三角形数记为an,计算a2﹣a1,a3﹣a2,a4﹣a3,…,由此推算,a100﹣a99=_____,a100=_____.
100 5050 【解析】根据题意可知: a2﹣a1=3﹣1=2; a3﹣a2=6﹣3=3; a4﹣a3=10﹣6=4; …; an﹣an﹣1=n. 所以a100﹣a99=100. ∵(a2﹣a1)+(a3﹣a2)+(a4﹣a3)+…+(an﹣an﹣1) =2+3+4+…+n =﹣1=an﹣a1, ∴a100==5050. 故...
练习册系列答案
相关题目
已知二次函数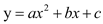 自变量x与函数值y之间满足下列数量关系:
自变量x与函数值y之间满足下列数量关系:
x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
y | 15 | 8 | 3 | 0 | -1 | 0 | 3 | 8 | 15 |
那么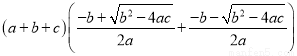 的值为( )
的值为( )
A. -2 B. -1 C. 0 D. 1
A 【解析】根据表中的数据可知,抛物线的对称轴是x=?=1,则?=2.当x=1时,y=a+b+c=?1, 则(a+b+c) =? (a+b+c)=2×(?1)=?2, 故选:A.

 有四个整数解,则a的取值范围是________________.
有四个整数解,则a的取值范围是________________.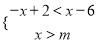 的解集是x>4,那么m的取值范围是 ( ).
的解集是x>4,那么m的取值范围是 ( ).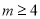 B.
B. 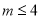 C. m<4 D. m=4
C. m<4 D. m=4
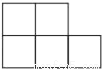 B.
B. 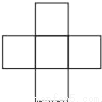 C.
C.  D.
D. 
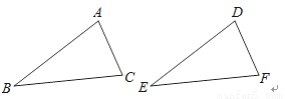
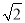 的倒数是( )
的倒数是( )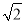 B. -
B. -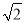 C. -
C. -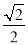 D.
D.