题目内容
8.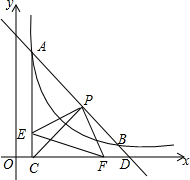 如图,一条直线与反比例函数y=$\frac{k}{x}$的图象交于A(1,4),B(4,n)两点,与x轴交于点D,AC⊥x轴,垂足为C.
如图,一条直线与反比例函数y=$\frac{k}{x}$的图象交于A(1,4),B(4,n)两点,与x轴交于点D,AC⊥x轴,垂足为C.(1)求反比例函数的解析式及D点的坐标;
(2)点P是线段AD的中点,点E,F分别从C,D两点同时出发,以每秒1个单位的速度沿CA,DC运动,到点A,C时停止运动,设运动的时间为t(s).
①求证:PE=PF.
②若△PEF的面积为S,求S的最小值.
分析 (1)把点A(1,4)代入y=$\frac{k}{x}$求出k的值,即可得出反比例函数的解析式;求出点B的坐标,用待定系数法求出直线AB的解析式,容易求出D点的坐标;
(2)①证明△ACD为等腰直角三角形,得出∠ADC=45°,由等腰直角三角形的性质得出CP=PD,CP⊥AD,∠ADC=∠ACP,由SAS证明△ECP≌△FDP,即可得出PE=PF;
②由△ECP≌△FDP,得出∠EPC=∠FPD,得出∠EPF=∠CPD=90°,证出△EPF为等腰直角三角形,得出△PEF的面积S=$\frac{1}{2}$PE2,当PE⊥AC时,PE最小,求出PE的最小值,即可得出S的最小值.
解答 (1)解:把点A(1,4)代入y=$\frac{k}{x}$得:k=4,
∴反比例函数的解析式为:y=$\frac{4}{x}$;
把点B(4,n)代入得:n=1,
∴B(4,1)
设直线AB的解析式为y=kx+b,
把A(1,4),B(4,1)代入y=kx+b得:$\left\{\begin{array}{l}{k+b=4}\\{4k+b=1}\end{array}\right.$,
解得:k=-1,b=5,
∴直线AB的解析式为:y=-x+5,
当y=0时,x=5,
∴D点坐标为:(5,0);
(2)①证明:∵A(1,4),C(1,0 ),D(5,0),AC⊥x轴于C,
∴AC=CD=4,
∴△ACD为等腰直角三角形,
∴∠ADC=45°,
∵P为AD中点,
∴∠ACP=∠DCP=45°,CP=PD,CP⊥AD,
∴∠ADC=∠ACP,
∵点E,F分别从C,D两点同时出发,以每秒1个单位的速度沿CA,DC运动,
∴EC=DF,
在△ECP和△FDP中,$\left\{\begin{array}{l}{CP=PD}&{\;}\\{∠ECP=∠PDF}&{\;}\\{EC=DF}&{\;}\end{array}\right.$,
∴△ECP≌△FDP(SAS),
∴PE=PF;
②解:∵△ECP≌△FDP,
∴∠EPC=∠FPD,
∴∠EPF=∠CPD=90°,
∴△PEF为等腰直角三角形,
∴△PEF的面积S=$\frac{1}{2}$PE2,
∴△PEF的面积最小时,EP最小,
∵当PE⊥AC时,PE最小,
此时EP最小值=$\frac{1}{2}$CD=2,
∴△PEF的面积S的最小值=$\frac{1}{2}$×22=2.
点评 本题是反比例函数综合题目,考查了用待定系数法求反比例函数和一次函数的解析式、等腰直角三角形的判定与性质、全等三角形的判定与性质、三角形面积的计算等知识;本题难度较大,综合性强,特别是(2)中,需要证明三角形全等和等腰直角三角形才能得出结论.

 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
(1)你认为大米手机5月份的销售量必定是三个品牌手机中最高的吗?通过计算说明你的理由.
(2)若各品牌手机2015年4月的销售量如下:
| 手机品牌 | 芒果手机 | 四星手机 | 大米手机 |
| 销售量(台) | 200 | 80 | 120 |
| A. | 了解某种酸奶中钙的含量 | B. | 了解某班学生的课外作业时间 | ||
| C. | 公司招聘职员,对应聘人员的面试 | D. | 旅客上飞机前的安检 |
| A. | 2x-x=2 | B. | x•x4=2x5 | C. | x2y÷y=x2 | D. | (-2x)3=-6x3 |
| A. | (a+b)2=a2+b2 | B. | (-2ab3)2=-4a2b6 | C. | 3a2-2a3=a6 | D. | a3-a=a(a+1)(a-1) |
| A. | $\sqrt{3}$ | B. | $\frac{1}{\sqrt{3}}$ | C. | -$\frac{1}{\sqrt{3}}$ | D. | -$\frac{1}{3}$ |
| A. | 第一、二象限 | B. | 第一、三象限 | C. | 第二、四象限 | D. | 第三、四象限 |
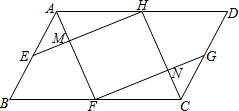 如图,在?ABCD中,E、F、G、H分别为AB、BC、CD、AD的中点,AF与EH交于点M,FG与CH交于点N.
如图,在?ABCD中,E、F、G、H分别为AB、BC、CD、AD的中点,AF与EH交于点M,FG与CH交于点N.