题目内容
19.若点M(a,b)在直线y=-$\frac{1}{2}$x+$\frac{5}{2}$上,则3a×9b÷27-2a-4b的值为-1.分析 将点M(a,b)代入y=-$\frac{1}{2}$x+$\frac{5}{2}$即可得出a+2b=5,代数式整理得到3a×9b÷27-2a-4b=3a+2b-3-2(a+2b),代入求得即可.
解答 解:∵点M(a,b)在直线y=-$\frac{1}{2}$x+$\frac{5}{2}$上,
∴b=-$\frac{1}{2}a$+$\frac{5}{2}$,
∴a+2b=5,
∵3a×9b÷27-2a-4b=3a+2b-3-2(a+2b),
∴3a×9b÷27-2a-4b=32-2×5=-1
故答案为-1,
点评 本题考查了一次函数图象上点的坐标特征,把点M代入解析式求得a+2b=5是解题的关键.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
9.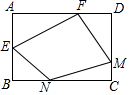 如图,在矩形ABCD中,E是AB边的中点,F在AD边上,M,N分别是CD,BC边上的动点,若AB=AF=2,AD=3,则四边形EFMN周长的最小值是( )
如图,在矩形ABCD中,E是AB边的中点,F在AD边上,M,N分别是CD,BC边上的动点,若AB=AF=2,AD=3,则四边形EFMN周长的最小值是( )
 如图,在矩形ABCD中,E是AB边的中点,F在AD边上,M,N分别是CD,BC边上的动点,若AB=AF=2,AD=3,则四边形EFMN周长的最小值是( )
如图,在矩形ABCD中,E是AB边的中点,F在AD边上,M,N分别是CD,BC边上的动点,若AB=AF=2,AD=3,则四边形EFMN周长的最小值是( )| A. | 2+$\sqrt{13}$ | B. | 2$\sqrt{2}$+2$\sqrt{5}$ | C. | 5+$\sqrt{5}$ | D. | 8 |
7.雾霾天气已经成为人们普遍关注的话题,雾霾不仅仅影响人们的出行,还影响着人们的健康,太原市会持续出现雾霾天气吗?在2016年2月周末休息期间,某校九年级1班综合实践小组的同学以“雾霾天气的主要成因”为主题,随机调查了太原市部分市民的观点,并对调查结果进行了整理,绘制了如下不完整的统计图表,观察并回答下列问题: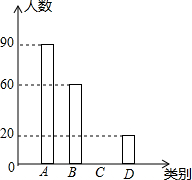
(1)请你求出本次被调查市民的人数及m,n的值,并补全条形统计图;
(2)若太原市有300万人口,请你估计持有A,B两类看法的市民共有多少人?
(3)学校要求小颖同学在A,B,C,D这四个雾霾天气的主要成因中,随机抽取两项作为课题研究的项目进行考察分析,请用画树状图或列表的方法,求出小颖同学刚好抽到B(汽车尾气排放),C(城中村燃煤问题)的概率.(用A,B,C,D表示各项目)

| 类别 | 雾霾天气的主要成因 | 百分比 |
| A | 工业污染 | 45% |
| B | 汽车尾气排放 | m |
| C | 城中村燃煤问题 | 15% |
| D | 其他(绿化不足等) | n |
(2)若太原市有300万人口,请你估计持有A,B两类看法的市民共有多少人?
(3)学校要求小颖同学在A,B,C,D这四个雾霾天气的主要成因中,随机抽取两项作为课题研究的项目进行考察分析,请用画树状图或列表的方法,求出小颖同学刚好抽到B(汽车尾气排放),C(城中村燃煤问题)的概率.(用A,B,C,D表示各项目)
14. 已知函数y=$\frac{m-1}{x}$(m≠0)的图象如图所示,有以下结论:①m<1;②在每个分支上y随x的增大而增大;③若点A(-2,a),点B(4,b)在图象上,则a<b;④若点P(x,y)在图象上,则点P(-x,-y)也在图象上,则下面选项正确的是( )
已知函数y=$\frac{m-1}{x}$(m≠0)的图象如图所示,有以下结论:①m<1;②在每个分支上y随x的增大而增大;③若点A(-2,a),点B(4,b)在图象上,则a<b;④若点P(x,y)在图象上,则点P(-x,-y)也在图象上,则下面选项正确的是( )
 已知函数y=$\frac{m-1}{x}$(m≠0)的图象如图所示,有以下结论:①m<1;②在每个分支上y随x的增大而增大;③若点A(-2,a),点B(4,b)在图象上,则a<b;④若点P(x,y)在图象上,则点P(-x,-y)也在图象上,则下面选项正确的是( )
已知函数y=$\frac{m-1}{x}$(m≠0)的图象如图所示,有以下结论:①m<1;②在每个分支上y随x的增大而增大;③若点A(-2,a),点B(4,b)在图象上,则a<b;④若点P(x,y)在图象上,则点P(-x,-y)也在图象上,则下面选项正确的是( )| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ①②③④ |
4.一组数据为1,5,3,4,5,6,这组数据的众数、中位数分为( )
| A. | 4,5 | B. | 5,4.5 | C. | 5,4 | D. | 3,2 |
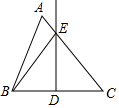 如图所示,△ABC中,DE是BC的垂直平分线,DE交AC于点E,连接BE,若BE=13,BC=10,则sinC=$\frac{12}{13}$.
如图所示,△ABC中,DE是BC的垂直平分线,DE交AC于点E,连接BE,若BE=13,BC=10,则sinC=$\frac{12}{13}$.