题目内容
9.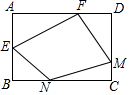 如图,在矩形ABCD中,E是AB边的中点,F在AD边上,M,N分别是CD,BC边上的动点,若AB=AF=2,AD=3,则四边形EFMN周长的最小值是( )
如图,在矩形ABCD中,E是AB边的中点,F在AD边上,M,N分别是CD,BC边上的动点,若AB=AF=2,AD=3,则四边形EFMN周长的最小值是( )| A. | 2+$\sqrt{13}$ | B. | 2$\sqrt{2}$+2$\sqrt{5}$ | C. | 5+$\sqrt{5}$ | D. | 8 |
分析 先延长EB至G,使BE=BG,延长FD到H,使DF=DH,连接GN,MH,根据M,N分别是CD,BC边上的动点,可得当点G、N、M、H在同一直线上时,GN+MN+MH=GH最短,即EN+MN+MF最短,再根据勾股定理求得GH和EF的长,即可得出四边形EFMN周长的最小值.
解答  解:如图所示,延长EB至G,使BE=BG,延长FD到H,使DF=DH,连接GN,MH,
解:如图所示,延长EB至G,使BE=BG,延长FD到H,使DF=DH,连接GN,MH,
∴BC垂直平分EG,CD垂直平分FH,
∴EN=GN,MF=MH,
∵E是AB边的中点,F在AD边上,AB=AF=2,AD=3,
∴EF长不变,AE=EB=BG=1,DF=DH=1,
即AG=3,AH=4,
∵M,N分别是CD,BC边上的动点,
∴当点G、N、M、H在同一直线上时,GN+MN+MH=GH最短,
即EN+MN+MF最短,
此时Rt△AGH中,GH=$\sqrt{A{G}^{2}+A{H}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴EN+MN+MF=5,
又∵Rt△AEF中,EF=$\sqrt{A{E}^{2}+A{F}^{2}}$=$\sqrt{5}$,
∴EN+MN+MF+EF=5+$\sqrt{5}$,
∴四边形EFMN周长的最小值是5+$\sqrt{5}$,
故选:C.
点评 本题考查了轴对称的性质以及勾股定理的运用,正确作出辅助线,确定EN+MN+MF的值最小时,M、N的位置是关键.凡是涉及最短距离的问题,一般要考虑线段的性质定理,多数情况要作点关于某直线的对称点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.某天的最高气温是5℃,最低气温是-4℃,则这一天气温的温差是( )
| A. | 1℃ | B. | -1℃ | C. | 9℃ | D. | -9℃ |
1.若代数式$\frac{\sqrt{x+1}}{x-2}$在实数范围内有意义,则实数x的取值范围是( )
| A. | x≥-1 | B. | x>2 | C. | x≠2 | D. | x≥-1且x≠2 |
18.-2017的相反数是( )
| A. | ±2017 | B. | -2017 | C. | 2017 | D. | -2018 |
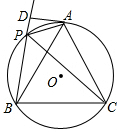 如图,⊙O是等边三角形ABC的外接圆,P是⊙O上的一个点,D是BP延长线上的一个点,且∠DAP=∠ABP,若AD=4,PD=2,则线段PA的长是$\sqrt{13}$+1.
如图,⊙O是等边三角形ABC的外接圆,P是⊙O上的一个点,D是BP延长线上的一个点,且∠DAP=∠ABP,若AD=4,PD=2,则线段PA的长是$\sqrt{13}$+1. 如图,直线a与b相交于点O,直线c⊥b,且垂足为O,若∠1=35°,则∠2=55°.
如图,直线a与b相交于点O,直线c⊥b,且垂足为O,若∠1=35°,则∠2=55°.