题目内容
10.如图①,在四边形ABCD中,AD∥BC,∠C=90°,CD=6cm.动点Q从点B出发,以1cm/S的速度沿BC运动到点C停止,同时,动点P也从B点出发,沿折线B→A→D运动到点D停止,且PQ⊥BC.设运动时间为t(s),点P运动的路程为y(cm),在直角坐标系中画出y关于t的函数图象为折线段OE和EF(如图②).已知点M(4,5)在线段OE上,则图①中AB的长是10cm.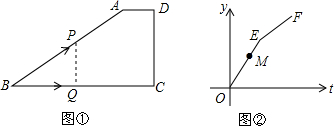
分析 设OE的解析式为y=kt,根据点M(4,5)可得到k=$\frac{5}{4}$,如图,当Q运动到G点时,点P运动到A点,BQ=t,AB=$\frac{5}{4}t$,AG=CD=6,根据勾股定理列方程即可.
解答 解:设OE的解析式为y=kt,
∵点M(4,5),
∴k=$\frac{5}{4}$,
如图,当Q运动到G点时,点P运动到A点,BQ=t,AB=$\frac{5}{4}t$,
∵AG⊥BC,
∴四边形ADCG是矩形,
∴AG=DC=6,
∴AB2=BG2+AG2,
∴($\frac{5}{4}t$)2=t2+62,
解得:t=8,
∴AB=$\frac{5}{4}$×8=10(cm).
点评 本题主要考查了动点函数问题的图象,能够结合图①②理清思路是解决问题的关键.

练习册系列答案
相关题目
2.关于x的方程x+2=ax的解为( )
| A. | 正数 | B. | 负数 | C. | 0 | D. | 以上答案都不对 |
19.二次函数y=ax2+bx+1(a>1)的图象与x轴两个交点的横坐标分别为x1,x2(x1<x2),一元二次方程a2x2+bx+1=0有两个实数根x3,x4(x3<x4),则x1,x2,x3,x4的大小关系是( )
| A. | x1<x2<x3<x4 | B. | x1<x3<x4<x2 | C. | x3<x1<x2<x4 | D. | x3<x4<x1<x2 |
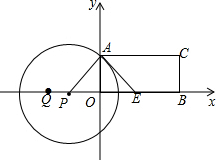 如图,矩形ABCD,A(0,3)、B(6,0),点E在OB上,∠AEO=45°,点P从点Q(-4,0)出发,沿x轴向右以每秒1个单位长的速度运动,运动时间为t秒.
如图,矩形ABCD,A(0,3)、B(6,0),点E在OB上,∠AEO=45°,点P从点Q(-4,0)出发,沿x轴向右以每秒1个单位长的速度运动,运动时间为t秒.