题目内容
2.已知实数a、b、c满足$\frac{1}{2}$|a-b|+$\sqrt{2b-c}$+c2-c+$\frac{1}{4}$=0,求a(b+c)的值.分析 根据非负数的性质列方程求出a、b、c的值,然后代入代数式进行计算即可得解.
解答 解:$\frac{1}{2}$|a-b|+$\sqrt{2b-c}$+(c-$\frac{1}{2}$)2=0,
所以,a-b=0,2b-c=0,c-$\frac{1}{2}$=0,
解得a=b=$\frac{1}{4}$,c=$\frac{1}{2}$,
所以,a(b+c)=$\frac{1}{4}$×($\frac{1}{4}$+$\frac{1}{2}$)=$\frac{1}{4}$×$\frac{3}{4}$=$\frac{3}{16}$.
点评 本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
13.用尺规作图作一个角等于已知角的示意图如图所示,则说明∠A′OB′=∠AOB依据是( )


| A. | SAS | B. | ASA | C. | SSS | D. | AAS |
7.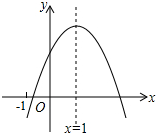 二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,则下列结论中错误的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,则下列结论中错误的是( )
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,则下列结论中错误的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,则下列结论中错误的是( )| A. | abc<0 | B. | a-b+c<0 | C. | b2-4ac>0 | D. | 3a+c>0 |
14.若a<b,则下列各式中一定正确的是( )
| A. | a-b>0 | B. | -a>-b | C. | a+2>b+2 | D. | ac<bc |
11.不等式组 $\left\{\begin{array}{l}{x+2>0}\\{x-2≤2}\end{array}\right.$ 的解集是( )
| A. | x>-2 | B. | x≤4 | C. | -2<x≤4 | D. | 无解 |
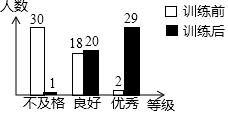 某校九年级700名学生在2016年中考体育考试前对跑步进行了强化训练,在训练前后进行了二次测试,测试成绩都以同一标准(10分为满分)划分成“不及格(7分及以下)”、“良好(9分或8分)”和“优秀(10分)”三个等级.为了了解强化训练的效果,用随机方式抽取了九年级学生中50名学生的前后两次测试成绩的等级,并绘制成如图所示的统计图,试结合图形信息回答下列问题:
某校九年级700名学生在2016年中考体育考试前对跑步进行了强化训练,在训练前后进行了二次测试,测试成绩都以同一标准(10分为满分)划分成“不及格(7分及以下)”、“良好(9分或8分)”和“优秀(10分)”三个等级.为了了解强化训练的效果,用随机方式抽取了九年级学生中50名学生的前后两次测试成绩的等级,并绘制成如图所示的统计图,试结合图形信息回答下列问题: