题目内容
9.已知关于x的一元二次方程x2+mx+3=0的一个根为-1,求它的另一个根及的m值.分析 根据一元二次方程的解的定义,将x=-1代入一元二次方程x2+mx+3=0,求得m值,然后将m值代入原方程,利用根与系数的关系求另一根.
解答 解:设方程的另一根是x2.
∵一元二次方程x2+mx+3=0的一个根为-1,
∴x=-1是原方程的解,
∴1-m+3=0,
解得m=4;
又由韦达定理,得-1×x2=3,
∴x2=-3,即原方程的另一根是-3.
点评 本题考查了一元二次方程的解、根与系数的关系.另外,本题也可以设方程的另一根是x2.然后利用根与系数的关系来求另一个根及m的值.

练习册系列答案
相关题目
19.下列命题是假命题的有( )
①若a2=b2,则a=b;
②一个角的余角大于这个角;
③若a,b是有理数,则|a+b|=|a|+|b|;
④如果∠A=∠B,那∠A与∠B是对顶角.
①若a2=b2,则a=b;
②一个角的余角大于这个角;
③若a,b是有理数,则|a+b|=|a|+|b|;
④如果∠A=∠B,那∠A与∠B是对顶角.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.抛物线y=3x2,y=-3x2,y=x2+3共有的性质是( )
| A. | 开口向上 | B. | 对称轴是y轴 | ||
| C. | 都有最高点 | D. | y随x的增大而增大 |
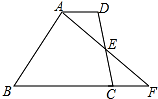 如图,在四边形ABCD中,AD∥BC,E为CD中点,连接AE并延长交BC的延长线于点F.
如图,在四边形ABCD中,AD∥BC,E为CD中点,连接AE并延长交BC的延长线于点F. 反比例函数y=$\frac{k-3}{x}$的图象如图所示,则实数k的取值范围是k>3.
反比例函数y=$\frac{k-3}{x}$的图象如图所示,则实数k的取值范围是k>3. 如图,△ABC中,AB与BC的夹角是∠B,∠A的对边是CB,∠A、∠C的公共边是AC.
如图,△ABC中,AB与BC的夹角是∠B,∠A的对边是CB,∠A、∠C的公共边是AC.