题目内容
3.为了让某市的山更绿、水更清,2014年市委、市政府提出了确保到2016年实现全市森林覆盖率达到63%的目标,已知2014年该市森林覆盖率为60%.设从2014年起森林覆盖率的年平均增长率为x,则可列方程( )| A. | 60(1+2x)=63% | B. | 60(1+2x)=63 | C. | 60(1+x)2=63% | D. | 60(1+x)2=63 |
分析 等量关系为:2014年全市森林覆盖率×(1+增长率)2=2016年全市森林覆盖率,把相关数值代入即可.
解答 解:2015年全市森林覆盖率为60%×(1+x),
2016年全市森林覆盖率为60%×(1+x)×(1+x)=63%×(1+x)2,
可列方程为60%×(1+x)2=63%,
故选D.
点评 本题考查了求平均变化率的方法.若设变化前的量为a,变化后的量为b,平均变化率为x,则经过两次变化后的数量关系为a(1±x)2=b.

练习册系列答案
相关题目
13.若整数k满足k<$\sqrt{90}$<k+1,则k的值是( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
14.某牧场为估计该地山羊的只数,先捕捉20只山羊给它们分别作上标志,然后放回,待有标志的山羊完全混合于山羊群后,第二次捕捉80只山羊,发现其中2只有标志.从而估计该地区有山羊( )
| A. | 400只 | B. | 600只 | C. | 800只 | D. | 1000只 |
18.已知P是△ABC内一点,连接PA,PB,PC,且PA=PB=PC,则P点一定是( )
| A. | △ABC的三条中线的交点 | B. | △ABC的三条内角平分线的交点 | ||
| C. | △ABC的三条高的交点 | D. | △ABC的三边的中垂线的交点 |
15. 2015年7月31日,在马来西亚吉隆坡举行的国际奥委会第128次全会上,国际奥委会主席巴赫宣布:中国北京获得2022年第24届冬季奥林匹克运动会主办权.学校想知道学生对相关信息的了解程度,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A、B、C、D四类.其中,A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”,D类表示“不太了解”,划分类别后的数据整理如表:
2015年7月31日,在马来西亚吉隆坡举行的国际奥委会第128次全会上,国际奥委会主席巴赫宣布:中国北京获得2022年第24届冬季奥林匹克运动会主办权.学校想知道学生对相关信息的了解程度,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A、B、C、D四类.其中,A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”,D类表示“不太了解”,划分类别后的数据整理如表:
请你根据所提供的信息解答下列问题:
(1)表中的a=0.3,b=6;
(2)根据表中数据,求扇形统计图中类别为B的学生数所对应的扇形圆心角的度数;
(3)我校有学生3600名,根据调查结果估计该校学生中类别为C的人数约为多少?
 2015年7月31日,在马来西亚吉隆坡举行的国际奥委会第128次全会上,国际奥委会主席巴赫宣布:中国北京获得2022年第24届冬季奥林匹克运动会主办权.学校想知道学生对相关信息的了解程度,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A、B、C、D四类.其中,A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”,D类表示“不太了解”,划分类别后的数据整理如表:
2015年7月31日,在马来西亚吉隆坡举行的国际奥委会第128次全会上,国际奥委会主席巴赫宣布:中国北京获得2022年第24届冬季奥林匹克运动会主办权.学校想知道学生对相关信息的了解程度,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A、B、C、D四类.其中,A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”,D类表示“不太了解”,划分类别后的数据整理如表:| 类别 | A | B | C | D |
| 频数 | 30 | 40 | 24 | b |
| 频率 | a | 0.4 | 0.24 | 0.06 |
(1)表中的a=0.3,b=6;
(2)根据表中数据,求扇形统计图中类别为B的学生数所对应的扇形圆心角的度数;
(3)我校有学生3600名,根据调查结果估计该校学生中类别为C的人数约为多少?
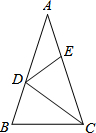 如图,在△ABC中,∠A=36°,AB=AC,CD是△ABC的角平分线.若在边AC上截取CE=CB,连接DE,则图中等腰三角形共有( )
如图,在△ABC中,∠A=36°,AB=AC,CD是△ABC的角平分线.若在边AC上截取CE=CB,连接DE,则图中等腰三角形共有( ) 如图,已知△ABC,用尺规作出△ABC的一条中位线.(保留作图痕迹,不写作法)
如图,已知△ABC,用尺规作出△ABC的一条中位线.(保留作图痕迹,不写作法)