题目内容
14.今有鸡翁一,值钱五,鸡母一,值钱三,鸡雏三,值钱一,百钱买百鸡,鸡翁,鸡母,鸡雏都买,可各买多少?分析 设鸡翁、鸡母、鸡雏分别为x、y、z,则有$\left\{\begin{array}{l}{x+y+z=100}\\{5x+3y+\frac{1}{3}z=100}\end{array}\right.$,通过消元,将问题转化为求二元一次不定方程的非负整数解.
解答 解:设鸡翁有x只,鸡母有y只,鸡雏有z只,根据题意,得
$\left\{\begin{array}{l}{x+y+z=100}\\{5x+3y+\frac{1}{3}z=100}\end{array}\right.$,
整理得:7x+4y=100.
x=$\frac{100-4y}{7}$=$\frac{4(25-y)}{7}$,
∵x≥0,y≥0,且都是自然数,
∴$\frac{25-y}{7}$≥0,
∴y≤25,25-y是7的倍数,且三种鸡都有买,
∴25-y=7,14,21,
y=18,11,4
∴共有3种情况:
①鸡翁4只,鸡母18只,鸡雏78只;
②鸡翁8只,鸡母11只,鸡雏81只;
③鸡翁12只,鸡母4只,鸡雏84只.
点评 本题考查列三元一次不定方程解古代数学问题的运用,不定方程组的解法的运用,解答时根据条件建立方程是关键.

练习册系列答案
相关题目
6.设a=2$\sqrt{3}$-1,a在两个相邻整数之间,则这两个整数是( )
| A. | 1和2 | B. | 2和3 | C. | 3和4 | D. | 4和5 |
3.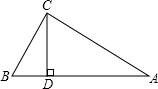 如图,已知Rt△ABC中,∠ACB=90°,CD是高,∠A=30°,BD=2cm,求AB的长( )
如图,已知Rt△ABC中,∠ACB=90°,CD是高,∠A=30°,BD=2cm,求AB的长( )
 如图,已知Rt△ABC中,∠ACB=90°,CD是高,∠A=30°,BD=2cm,求AB的长( )
如图,已知Rt△ABC中,∠ACB=90°,CD是高,∠A=30°,BD=2cm,求AB的长( )| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
 如图,用18米长的木方做一个有一条横档的矩形窗子,窗子的宽不能超过2米.为使透进的光线最多,则窗子的长、宽应各为多少米?
如图,用18米长的木方做一个有一条横档的矩形窗子,窗子的宽不能超过2米.为使透进的光线最多,则窗子的长、宽应各为多少米? 如图,已知OB是∠AOC的角平分线,OD是∠COE的角平分线,
如图,已知OB是∠AOC的角平分线,OD是∠COE的角平分线,