题目内容
(1)等边三角形的边长为2
,求他的中线长,并求出其面积.
(2)等边三角形的一条角平分线长为
,求这个三角形的边长.
| 3 |
(2)等边三角形的一条角平分线长为
| 3 |
考点:等边三角形的性质
专题:
分析:(1)根据等边三角形三线合一的性质可以求得中线AD的长度,根据BC和AD即可求得三角形的面积.
(2)根据等边三角形三线合一的性质,等边三角形一条边上的中线就是这边的高,再根据等边三角形的高等于边长的
倍列式计算即可得解.
(2)根据等边三角形三线合一的性质,等边三角形一条边上的中线就是这边的高,再根据等边三角形的高等于边长的
| ||
| 2 |
解答: 解:(1)∵AD是△ABC的中线,
解:(1)∵AD是△ABC的中线,
∴D为BC的中点,BD=DC=
,AD⊥BC,
在Rt△ABD中,AB=2
,BD=
,
∴AD=
=3,
∴等边△ABC的面积为
BC•AD=
×2
×3=3
.
(2)∵等边三角形的一条角平分线长为
,
∴它的一条高的长为
,
设等边三角形的边长=x,
∴
=
x,
解得x=2.
 解:(1)∵AD是△ABC的中线,
解:(1)∵AD是△ABC的中线,∴D为BC的中点,BD=DC=
| 3 |
在Rt△ABD中,AB=2
| 3 |
| 3 |
∴AD=
| AB2-BD2 |
∴等边△ABC的面积为
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
(2)∵等边三角形的一条角平分线长为
| 3 |
∴它的一条高的长为
| 3 |
设等边三角形的边长=x,
∴
| 3 |
| ||
| 2 |
解得x=2.
点评:本题考查了勾股定理在直角三角形中的运用,考查了三角形面积的计算,考查了等边三角形各边长相等的性质,等边三角形三线合一的性质是解题不到关键.

练习册系列答案
相关题目
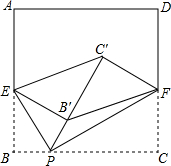 如图,已知,正方形纸片ABCD的边长为4,点P在BC边上,BP=1,点E在AB边上,且∠BPE=60°,沿PE翻折△EBP得到△EB′P. F是CD边上一点,沿PF翻折△FCP得到△FC′P,使点Cˊ落在射线PBˊ上.
如图,已知,正方形纸片ABCD的边长为4,点P在BC边上,BP=1,点E在AB边上,且∠BPE=60°,沿PE翻折△EBP得到△EB′P. F是CD边上一点,沿PF翻折△FCP得到△FC′P,使点Cˊ落在射线PBˊ上.
