题目内容
13. 阅读下面的材料:
阅读下面的材料:在平面几何中,我们学过两条直线平行的定义.下面就两个一次函数的图象所确定的两条直线给出它们平行的定义:设一次函数y=k1x+b1(k1≠0)的图象为直线l1,一次函数y=k2x+b2(k2≠0)的图象为直线l2,若k1=k2,且b1≠b2,我们就称直线l1与直线l2互相平行.
解答下面的问题:
(1)已知正比例函数y=-x的图象为直线l1,求过点P(1,3)且与已知直线l1平行的直线l2的函数表达式;
(2)设直线l2分别与y轴、x轴交于点A、B,求l1和l2两平行线之间的距离;
(3)若Q为OA上一动点,求QP+QB的最小值时Q点的坐标为Q(0,$\frac{12}{5}$).
(4)在x轴上找一点M,使△BMP为等腰三角形,求M的坐标.(直接写出答案)
分析 (1)设直线l2的函数表达式为y=-x+b,把P坐标代入求出b的值,即可确定出表达式;
(2)过O作ON垂直于AB,此时ON为两平行线间的距离,根据三角形AOB为等腰直角三角形,求出ON的长即可;
(3)找出B关于y轴的对称点B′(-4,0),连接PB′,与y轴交于点Q,连接PQ,此时QP+QB最小,利用待定系数法求出直线B′P解析式,找出此直线与y轴交点即为Q坐标;
(4)如图2所示,分三种情况考虑:当PM1=PB时;当PM2=BM2时,M2为线段PB垂直平分线与x轴的交点;当PB=M3B时,分别求出M坐标即可.
解答 解:(1)根据正比例函数y=-x的图象为直线l1,设直线l2的函数表达式为y=-x+b,
把P(1,3)代入得:3=-1+b,即b=4,
则过点P(1,3)且与已知直线l1平行的直线l2的函数表达式为y=-x+4;
(2)过O作ON⊥AB,如图1所示,ON为l1和l2两平行线之间的距离,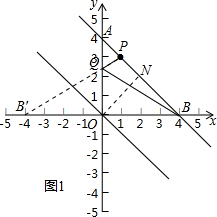
对于直线y=-x+4,令x=0,得到y=4;令y=0,得到x=4,
∴A(0,4),B(4,0),即OA=OB=4,
∵△ABC为等腰直角三角形,
∴AB=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$,且ON为斜边上的中线,
∴ON=$\frac{1}{2}$AB=2$\sqrt{2}$,
则l1和l2两平行线之间的距离为2$\sqrt{2}$;
(3)找出B关于y轴的对称点B′(-4,0),连接PB′,与y轴交于点Q,连接PQ,此时QP+QB最小,
设直线B′P的解析式为y=mx+n,
把B′和P坐标代入得:$\left\{\begin{array}{l}{-4m+n=0}\\{m+n=3}\end{array}\right.$,
解得:m=$\frac{3}{5}$,n=$\frac{12}{5}$,
∴直线B′P的解析式为y=$\frac{3}{5}$x+$\frac{12}{5}$,
令x=0,得到y=$\frac{12}{5}$,即Q(0,$\frac{12}{5}$);
故答案为:Q(0,$\frac{12}{5}$);
(4)如图2所示,分三种情况考虑: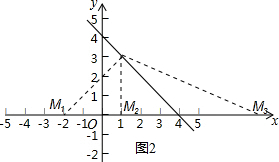
当PM1=PB时,由对称性得到M1(-2,0);
当PM2=BM2时,M2为线段PB垂直平分线与x轴的交点,
∵直线PB的解析式为y=-x+4,且线段PB中点坐标为(2.5,1.5),
∴线段PB垂直平分线解析式为y-1.5=x-2.5,即y=x-1,
令y=0,得到x=1,即M2(1,0);
当PB=M3B=$\sqrt{(4-1)^{2}+(0-3)^{2}}$=3$\sqrt{2}$时,OM3=OB+BM3=3+3$\sqrt{2}$,此时M3(3+3$\sqrt{2}$,0),
综上,M的坐标为(-2,0)或(1,0)或(3+3$\sqrt{2}$,0).
点评 此题属于一次函数综合题,涉及的知识有:待定系数法确定一次函数解析式,两直线垂直及平行时斜率满足的关系,坐标与图形性质,等腰三角形的性质,熟练掌握待定系数法是解本题的关键.

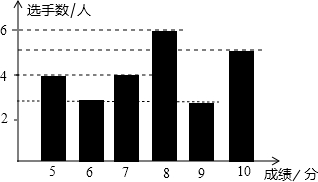 某校举行学生“爱校•爱家•爱国”主题演讲比赛,某同学将选手们的得分进行统计,绘制成如图所示的得分条形图下列四个判断:
某校举行学生“爱校•爱家•爱国”主题演讲比赛,某同学将选手们的得分进行统计,绘制成如图所示的得分条形图下列四个判断:①共有10人得6分;
②得5分和7分的人数一样多;
③8名选手的成绩高于8分;
④共有25名选手参赛.
其中正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 在Rt△ABC中,∠ABC=45°,F为BC中点,BE平分∠ABC交AF于G,交AC于E,CD⊥BE于D.有以下判断:①BF=CF;②∠ABE=∠DCE;③AE=AG;④BE=2CD;⑤CE=$\sqrt{2}$AG;⑥CE=BG.其中正确的判断个数是( )
在Rt△ABC中,∠ABC=45°,F为BC中点,BE平分∠ABC交AF于G,交AC于E,CD⊥BE于D.有以下判断:①BF=CF;②∠ABE=∠DCE;③AE=AG;④BE=2CD;⑤CE=$\sqrt{2}$AG;⑥CE=BG.其中正确的判断个数是( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
| A. | m-2>n-2 | B. | $\frac{m}{2}>\frac{n}{2}$ | C. | -2m>-2n | D. | m+2>n+2 |
 在平面直角坐标系中,第1个正方形ABCD的位置如图所示,点A的坐标为(2,0),点D的坐标为(0,4),延长CB交x轴于点A1,作第2个正方形A1B1C1C;延长C1B1交x轴于点A2,作第3个正方形A2B2C2C1…按这样的规律进行下去,第2个正方形的面积为45;第2015个正方形的面积为20×$(\frac{9}{4})$2014.
在平面直角坐标系中,第1个正方形ABCD的位置如图所示,点A的坐标为(2,0),点D的坐标为(0,4),延长CB交x轴于点A1,作第2个正方形A1B1C1C;延长C1B1交x轴于点A2,作第3个正方形A2B2C2C1…按这样的规律进行下去,第2个正方形的面积为45;第2015个正方形的面积为20×$(\frac{9}{4})$2014.
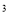 (y-x)
(y-x) 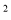 (x-y)+2(x-y)
(x-y)+2(x-y)