题目内容
12.化简:$\frac{4}{\sqrt{2}+2}$+$\frac{4}{2+\sqrt{6}}$+$\frac{4}{\sqrt{6}+\sqrt{8}}$+…$\frac{4}{\sqrt{2n}+\sqrt{2n-2}}$.
分析 直接将原式分母有理化,进而求出答案.
解答 解:原式=4[$\frac{2-\sqrt{2}}{(2+\sqrt{2})(2-\sqrt{2})}$+$\frac{\sqrt{6}-2}{(\sqrt{6}+2)(\sqrt{6}-2)}$+$\frac{\sqrt{8}-\sqrt{6}}{(\sqrt{8}+\sqrt{6})(\sqrt{8}-\sqrt{6})}$+$\frac{\sqrt{2n}-\sqrt{2n-2}}{(\sqrt{2n}+\sqrt{2n-2})(\sqrt{2n}-\sqrt{2n-2})}$
=2(2-$\sqrt{2}$+$\sqrt{6}$-2+$\sqrt{8}$-$\sqrt{6}$+…+$\sqrt{2n}$-$\sqrt{2n-2}$)
=-2$\sqrt{2}$+2$\sqrt{2n}$.
点评 此题主要考查了二次根式的混合运算等知识,正确化简二次根式是解题关键.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
2. 如图,一只蚂蚁沿边长为1的正方体表面从点A爬到点B,则它走过的路程最短为( )
如图,一只蚂蚁沿边长为1的正方体表面从点A爬到点B,则它走过的路程最短为( )
 如图,一只蚂蚁沿边长为1的正方体表面从点A爬到点B,则它走过的路程最短为( )
如图,一只蚂蚁沿边长为1的正方体表面从点A爬到点B,则它走过的路程最短为( )| A. | $\sqrt{3}$ | B. | 5 | C. | 3 | D. | $\sqrt{5}$ |
17.如图①,在平面直角坐标系中,平行四边形ABCD在第一象限,且AB∥x轴,直线y=-x从原点出发沿x轴正方向平移,被平行四边形ABCD截得的线段EF的长度l与平移的距离m的函数图象如图②,那么平行四边形ABCD的面积为( )
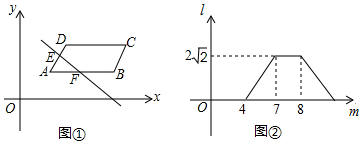

| A. | 4 | B. | $4\sqrt{2}$ | C. | 8 | D. | $8\sqrt{2}$ |
20.点A(-1,2)绕坐标原点O逆时针方向旋转90°得到的点A'的坐标是( )
| A. | (-2,-1) | B. | (2,-1) | C. | (1,-2) | D. | (2,1) |

 如图,在边长为3的正方形ABCD中,点E是BC边上的点,BE=1,∠AEP=90°,且EP交正方形外角的平分线CP于点P,交边CD于点F.
如图,在边长为3的正方形ABCD中,点E是BC边上的点,BE=1,∠AEP=90°,且EP交正方形外角的平分线CP于点P,交边CD于点F.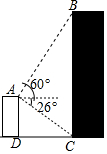 如图所示,小明在自家楼顶上的点A处测量建在与小明家楼房同一水平线上邻居的电梯楼的高度,测得电梯楼顶部B处的仰角为60°,底部C处的俯角为26°,已知小明家楼房的高度AD=15米,求电梯楼的高度BC.(结果精确到0.1米,参考数据:$\sqrt{3}$≈1.73,sin26°≈0.44,cos26°≈0.90,tan26°≈0.49)
如图所示,小明在自家楼顶上的点A处测量建在与小明家楼房同一水平线上邻居的电梯楼的高度,测得电梯楼顶部B处的仰角为60°,底部C处的俯角为26°,已知小明家楼房的高度AD=15米,求电梯楼的高度BC.(结果精确到0.1米,参考数据:$\sqrt{3}$≈1.73,sin26°≈0.44,cos26°≈0.90,tan26°≈0.49)