题目内容
9．若a＜0，且a2b＜0，a3b3＞0；已知|a|=3，|b|=5且a3＜0，b2＞0，则3a+2b的值为1或-19．分析 由a＜0，且a2b＜0，得出b＜0，进一步计算得出答案即可；
由|a|=3，|b|=5且a3＜0，b2＞0，得出a=-3，b=±5，由此代入求得答案即可．
解答 解：∵a＜0，且a2b＜0，
∴b＜0，
∴a3b3＞0；
∵|a|=3，|b|=5，
∴a=±3，b=±5，
∵a3＜0，
∴a＜0，
∴a=-3，b=±5，
∴3a+2b=1或-19．
故答案为：＞，1或-19．
点评 此题考查代数式求值，绝对值的意义，乘方的意义，正确判定字母的符号是解决问题的关键．
练习册系列答案
相关题目
14．填表：
| 单项式 | -$\frac{{a}^{2}{b}^{3}c}{2}$ | -0.5xyz2 | m | 0 | 3a2b |
| 系数 | -$\frac{1}{2}$ | -0.5 | 1 | 0 | 3 |
| 次数 | 6 | 4 | 1 | 0 | 3 |
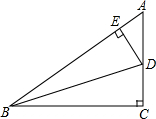在Rt△ABC中，BD平分∠ABC，DE⊥AB于E；