题目内容
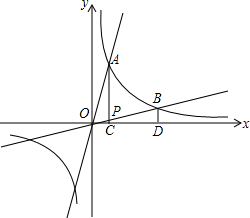 已知反比例函数y=
已知反比例函数y=| k |
| x |
(1)求m的值及反比例函数的解析式;
(2)若正比例函数y=
| 1 |
| 4 |
| 4 |
| x |
| 1 |
| 4 |
(3)联结AB,求△AOB的面积.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)根据自变量的值,可得相应的函数值,根据待定系数法,可得函数解析式;
(2)根据自变量的值,可得相应的函数值,即P点坐标,根据联立y=
x与反比例函数y=
,可的方程组,根据解方程组,可得B点坐标,根据线段的和差,可得BD、CD的长,根据梯形的面积公式,可得答案;
(3)根据勾股定理,可得OB的长,根据点到直线的距离公式,可得AE的长,根据三角形的面积公式,可得答案.
(2)根据自变量的值,可得相应的函数值,即P点坐标,根据联立y=
| 1 |
| 4 |
| 4 |
| x |
(3)根据勾股定理,可得OB的长,根据点到直线的距离公式,可得AE的长,根据三角形的面积公式,可得答案.
解答:解:(1)把A(1,m)代入y=4x
∴m=4,
把A(1,4)代入y=
,得
k=xy=4,
∴反比例函数的解析式y=
;
(2)把x=1代入y=
x,则y=
∴P(1,
),
∴PC=
.
联立y=
x与反比例函数y=
,得
,解得
,即B(4,1)
∴BD=1,CD=OD-OC=3
S梯形PBDC=
(PC+BD)•CD=
×(
+1)×3=
;
(3)如图:连接AB,作AE⊥OB与E点,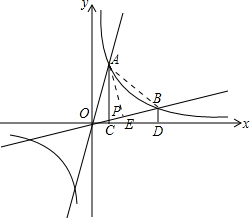 ,
,
由勾股定理,得OB=
=
=
,
由点到直线的距离公式,得AE=
=
,
由三角形的面积,得S=
OB•AE=
×
×
=
.
∴m=4,
把A(1,4)代入y=
| k |
| x |
k=xy=4,
∴反比例函数的解析式y=
| 4 |
| x |
(2)把x=1代入y=
| 1 |
| 4 |
| 1 |
| 4 |
∴P(1,
| 1 |
| 4 |
∴PC=
| 1 |
| 4 |
联立y=
| 1 |
| 4 |
| 4 |
| x |
|
|
∴BD=1,CD=OD-OC=3
S梯形PBDC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 15 |
| 8 |
(3)如图:连接AB,作AE⊥OB与E点,
 ,
,由勾股定理,得OB=
| OD2+BD2 |
| 42+12 |
| 17 |
由点到直线的距离公式,得AE=
|
| ||||
|
15
| ||
| 17 |
由三角形的面积,得S=
| 1 |
| 2 |
| 1 |
| 2 |
| 17 |
15
| ||
| 17 |
| 15 |
| 2 |
点评:本题考查了反比例函数与一次函数的交点问题,(1)利用了待定系数法求函数解析式,(2)利用了线段的和差,梯形的面积公式,(3)利用了点到直线的距离公式:P(x0,y0)到直线ax+by+c=0的距离是
,三角形的面积公式.
| |ax0+by0+c| | ||
|

练习册系列答案
相关题目
下列各对数中,数值相等的是( )
| A、-32与-23 |
| B、(-3)2与-32 |
| C、-23与(-2)3 |
| D、(-3×2)3与-3×23 |
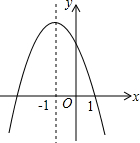 已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①a<0;②abc>0;③a+b+c=0;④a-b+c>0;⑤4a-2b+c<0;⑥ax2+bx+c<0的解集是x>1.其中正确的有( )
已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①a<0;②abc>0;③a+b+c=0;④a-b+c>0;⑤4a-2b+c<0;⑥ax2+bx+c<0的解集是x>1.其中正确的有( )| A、3个 | B、4个 | C、5个 | D、6个 |
几个棱长为1的小正方体组成的几何体,从正面、左面、上面看到的形状图如图所示,则这个几何体的表面积为( )


| A、7 | B、11 | C、14 | D、22 |
已知等腰三角形一边长为4,周长为10,则另两边长分别为( )
| A、4,2 | B、3,3 |
| C、4,2或3,3 | D、以上都不对 |
如果上升3米记作“+3”米,那么下降2米记作( )米.
| A、-2 | B、+5 | C、-5 | D、+2 |
蜗牛在井里距井口1米处,它每天白天向上爬行30cm,但每天晚上又下滑20cm.蜗牛爬出井口需要的天数是( )
| A、7 | B、8 | C、9 | D、10 |