题目内容
5.若关于x、y的方程mx+ny=8的两个解为$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$和$\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$,则m=8,n=8.分析 把方程的解代入方程可得到关于m、n的方程组,解方程组即可.
解答 解:
∵关于x、y的方程mx+ny=8的两个解为$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$和$\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$,
∴$\left\{\begin{array}{l}{2m-n=8}\\{-m+2n=8}\end{array}\right.$,解$\left\{\begin{array}{l}{m=8}\\{n=8}\end{array}\right.$,
故答案为:8;8.
点评 本题主要考查二元一次方程解的定义,掌握方程的解满足方程是解题的关键.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
16.下列各数中,与8${\;}^{\frac{1}{2}}$-2${\;}^{\frac{1}{2}}$相等的是( )
| A. | 2${\;}^{\frac{1}{2}}$ | B. | 6${\;}^{\frac{1}{2}}$ | C. | 4${\;}^{\frac{1}{2}}$ | D. | 3 |
20.抛掷一枚质地均匀的硬币,连续3次都是正面向上,则关于第4次抛掷结果,下面叙述正确的是( )
| A. | P(正面向上)>P(反面向上) | B. | P(正面向上)<P(反面向上) | ||
| C. | P(正面向上)=P(反面向上) | D. | 无法确定 |
17.任意实数a,可用[a]表示不超过a的最大整数,如[4]=4,[$\sqrt{3}$]=1,已知[$\sqrt{n}$]=5,则下列n的值符合条件的是( )
| A. | n=5 | B. | n=18 | C. | n=28 | D. | n=36 |
14.已知等腰三角形的腰和底的长分别是一元二次方程x2-7x+10=0的两个根,则该三角形的周长是( )
| A. | 9 | B. | 12 | C. | 9或12 | D. | 不能确定 |
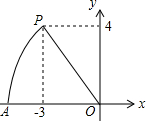 如图,在平面直角坐标系中,点P的坐标为(-3,4),以点O为圆心,以OP长为半径画弧,交x轴的负半轴于点A,则点A的横坐标为( )
如图,在平面直角坐标系中,点P的坐标为(-3,4),以点O为圆心,以OP长为半径画弧,交x轴的负半轴于点A,则点A的横坐标为( ) 如图,AD∥BE∥CF,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F,$\frac{AB}{BC}$=$\frac{2}{3}$,DE=6,则EF=9.
如图,AD∥BE∥CF,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F,$\frac{AB}{BC}$=$\frac{2}{3}$,DE=6,则EF=9.