题目内容
13.从-2、-1、3、6中随机抽取一个数记为a,再从剩下的三个数中任取一个记为b,则点(a,b)恰好在反比例函数y=-$\frac{6}{x}$的图象上的概率是$\frac{1}{3}$.分析 首先根据题意画出树状图,然后由树状图求得所有等可能的结果与点(a,b)恰好在反比例函数y=-$\frac{6}{x}$的图象上的情况,再利用概率公式即可求得答案.
解答 解:画树状图得: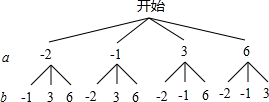
∵共有12种等可能的结果,点(a,b)恰好在反比例函数y=-$\frac{6}{x}$的图象上的有:(-2,3),(-1,6),(3,-2),(6,-1),
∴点(a,b)恰好在反比例函数y=-$\frac{6}{x}$的图象上的概率是:$\frac{4}{12}$=$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
3.用换元法解方程(x2+x)(x2+x-1)=6,如果设x2+x=y,则原方程可变形为( )
| A. | y2+y-6=0 | B. | y2-y-6=0 | C. | y2-y+6=0 | D. | y2-y-6=0 |
4.点m(-sin60°,cos60°)关于x轴的轴反射点的坐标是( )
| A. | ($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$) | B. | (-$\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$) | C. | (-$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$) | D. | (-$\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$) |
2.用公式法解一元二次方程3x2-2x+3=0时,首先要确定a、b、c的值,下列叙述正确的是( )
| A. | a=3,b=2,c=3 | B. | a=-3,b=2,c=3 | C. | a=3,b=2,c=-3 | D. | a=3,b=-2,c=3 |
 如图,点B在AM上,点D在AN上,且AB=AD,BC=CD,CE⊥AM于E,CF⊥AN于F.求证:BE=DF.
如图,点B在AM上,点D在AN上,且AB=AD,BC=CD,CE⊥AM于E,CF⊥AN于F.求证:BE=DF.