题目内容
 如图,点D是线段BC的中点,分别以点B,C为圆心,BC长为半径画弧,两弧相交于点A,连接AB,AC,AD,点E为AD上一点,连接BE,CE.
如图,点D是线段BC的中点,分别以点B,C为圆心,BC长为半径画弧,两弧相交于点A,连接AB,AC,AD,点E为AD上一点,连接BE,CE.
(1)求证:BE =CE;
=CE;
(2)以点E为圆心,ED长为半径画弧,分别交BE,CE于点F, G.若BC=4,∠EBD=30°,求图中阴影部分(扇形)的面积.
G.若BC=4,∠EBD=30°,求图中阴影部分(扇形)的面积.

(1)证明:∵点D是线段BC的中点,
∴BD=CD,
∵AB=AC=BC,
∴△ABC为等边三角形,
∴AD为BC的垂直平分线,
∴BE=CE;
(2)解:∵EB=EC,
∴∠EBC =∠ECB=30°,
=∠ECB=30°,
∴∠BEC=120°,
在Rt△BDE中,BD=BC=2,∠EBD=30°,
∴ED=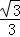 BD=
BD=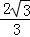 ,
,
∴阴影部分(扇形)的面积=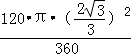 =π.10.解:如图3-172所示,作DH⊥BC于点H,∴DH=AB=2,CH=BC-BH=BC-AD=7-3=4.在Rt△CDH中,CD=
=π.10.解:如图3-172所示,作DH⊥BC于点H,∴DH=AB=2,CH=BC-BH=BC-AD=7-3=4.在Rt△CDH中,CD=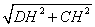 =
=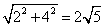 .∴S表=S圆锥侧+S圆柱侧+S底=π·DH·CD+2π·AB·AD+π·(AB)2=π×2×
.∴S表=S圆锥侧+S圆柱侧+S底=π·DH·CD+2π·AB·AD+π·(AB)2=π×2×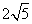 +2π×2×3+π×22=
+2π×2×3+π×22=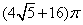 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 C.105° D.120°
C.105° D.120°
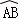 的长为( )
的长为( )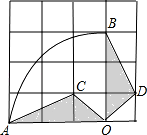
 .若将BD绕点B旋转后,点D落在BC延长线上的点D′处,点D经过的路径为
.若将BD绕点B旋转后,点D落在BC延长线上的点D′处,点D经过的路径为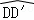 ,则图中阴影部分的面积是( )
,则图中阴影部分的面积是( )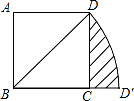
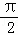 ﹣1 B
﹣1 B 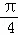 ﹣1 D π﹣2
﹣1 D π﹣2
 的顶点是(m,3),则m= ,c= .
的顶点是(m,3),则m= ,c= . 各边长
各边长 度都扩大2倍,则锐角A的正弦值和余弦值( )
度都扩大2倍,则锐角A的正弦值和余弦值( )