题目内容
如图,在△ABC中,∠A=36°,AB=AC,AB的垂直平分线OD交AB于点O,交AC于点D,连 接BD.有下列结论:①∠C=2∠A;②BD平分∠ABC;③ .其中正确的选 项是( )
.其中正确的选 项是( )
A.①③ B.②③
C. ①②③ D.①②

D 解析:本题综合考查了等腰三角形的性质、线段的垂直平分线与角的平分线的性质等知识.∵ ∠A=36°,AB=AC,∴ ∠C=∠ABC= 72°.∵ OD是AB的垂直平分线,∴ AD=BD,
∴ ∠A=∠ABD=36°,∴ ∠ABC=2∠ABD,∴ BD平分∠ABC,∴ ①和②都正确.
由BD平分∠ABC,∠ABC=72°,∴ ∠CBD=36°.
在△BCD中,∠BDC=180°-∠CBD-∠C=180°-36°-72°=72°,∴ ∠BDC=∠C,即BD=BC.
在Rt△BOD中,OB<BD,则OB<BC.作DE⊥BC,则OD=DE.
又 ,故
,故 >
> ,∴ ③错误.故选D.
,∴ ③错误.故选D.

练习册系列答案
相关题目

 B.
B.  C.
C.  D.
D. 
 如图1,在矩形ABCD中,动点P从点B出发,沿BC,CD,DA运动至点A停止.设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则△ABC的面积是
如图1,在矩形ABCD中,动点P从点B出发,沿BC,CD,DA运动至点A停止.设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则△ABC的面积是 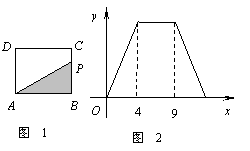 B.16
B.16 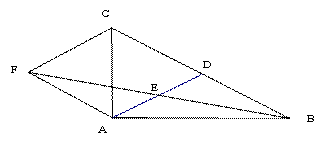 (2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论. B.4个 C.5个 D.6个
B.4个 C.5个 D.6个  如图,在△
如图,在△ 中,
中, ,
, 是∠
是∠ ,∠
,∠ ,则 ∠
,则 ∠ .
. ,
, ,
, ,
,  ;(2)
;(2) 互为倒数;(3)
互为倒数;(3) .
.