题目内容
8．
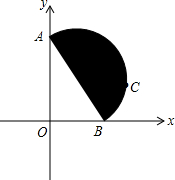如图，以AB为直径的半圆型铁片按如图所示的位置平放斜靠在坐标轴上，点C是半圆片弧AB上靠近B点的一个定点，现点A沿着y轴向终点O滑动，同时点B相应地沿着x轴正方向滑动．请判断：在滑动过程中，点C与点O距离的变化情况是（ ）| A． | 一直增大 | B． | 保持不变 | C． | 先减小后增大 | D． | 先增大后减小 |
分析 取AB的中点D，连接OD、CD，根据直角三角形斜边上的中线等于斜边的一半可得OD=$\frac{1}{2}$AB，然后根据两点之间线段最短可知O、D、C三点共线时OC最大，从而判断出点C与点O距离的变化情况．
解答 
解：如图，取AB的中点D，连接OD、CD，
∵△AOB是直角三角形，
∴OD=$\frac{1}{2}$AB，
由两点之间线段最短得，O、D、C三点共线时OC最大，
所以，点C与点O距离的先增大，然后减小．
故选D．
点评 本题考查了直角三角形的性质，两点之间线段最短的性质，最短距离的问题，作辅助线确定出OC的最大距离是解题的关键．
练习册系列答案
相关题目
13．若（x-3）（x+5）=x2+ax+b，则a+b的值是（ ）
| A． | -13 | B． | 13 | C． | 2 | D． | -15 |
如图，已知直线y=kx-6与抛物线y=ax2+bx-3相交于A，B两点，且点A坐标为（1，-4），点B在x轴上．
1．若|x+$\frac{1}{2}$|+（2y-1）2=0，则x2+y2的值是（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{8}$ | C． | -$\frac{1}{8}$ | D． | -$\frac{3}{8}$ |
如图，已知抛物线y=-$\frac{1}{4}$x2+bx+c与x轴相交于A、B两点，与y轴相交于点C（0，4），若已知A点的坐标为A（-2，0）．