题目内容
3．当关于x、y的方程组$\left\{\begin{array}{l}{x-y=3}\\{x+2y=a-3}\end{array}\right.$的解x为正数，y为非负数时，求出此时a的取值范围？分析 先用a表示出x、y的值，再由x为正数，y为非负数得出关于a的不等式，求出a的取值范围即可．
解答 解：解方程组$\left\{\begin{array}{l}{x-y=3}\\{x+2y=a-3}\end{array}\right.$得，$\left\{\begin{array}{l}{x=1+\frac{a}{3}}\\{y=\frac{a}{3}-2}\end{array}\right.$，
∵x为正数，y为非负数，
∴$\left\{\begin{array}{l}{1+\frac{a}{3}＞0}\\{\frac{a}{3}-2＜0}\end{array}\right.$，解得-3＜a＜6．
点评 本题考查的是解一元一次不等式组，根据题意列出关于a的不等式组是解答此题的关键．
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
如图，在△ABC中，点P在边AB上，则在下列四个条件中：①∠ACP=∠B；②∠APC=∠ACB；③AC2=AP•AB；④AB•CP=AP•CB，能满足△APC与△ACB相似的条件是（ ）
如图，在?ABCD中，AE⊥BC于E，AF⊥DC于F，∠ADC=60°，BE=2，CF=1，求?ABCD的面积．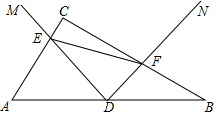
如图，△ABC中，∠ACB=90°，点D是AB中点，∠MDN=90°，DM交AC于点E，DN交BC于点F．
如图，BF，BE分别是∠ABC及其邻补角的平分线，AE⊥BE于点E，AF⊥BF于点F，四边形AEBF是矩形吗？请证明你的结论．