题目内容
12. 如图,BF,BE分别是∠ABC及其邻补角的平分线,AE⊥BE于点E,AF⊥BF于点F,四边形AEBF是矩形吗?请证明你的结论.
如图,BF,BE分别是∠ABC及其邻补角的平分线,AE⊥BE于点E,AF⊥BF于点F,四边形AEBF是矩形吗?请证明你的结论.
分析 由BF、BE是角平分线可得∠EBF是90°,进而由条件中的两个垂直可得两个直角,可得四边形AEBF是矩形;
解答 解:四边形AEBF是矩形.
理由:∵BF、BE分别是△ABC中∠B及它的外角的平分线,
∴∠GBE=∠ABE,∠ABF=∠FBC,
∵∠GBE+∠ABE+∠ABF+∠FBC=180°,
∴∠ABE+∠ABF=90°,
∴∠EBF=90°,
∵AE⊥BE,E为垂足,AF⊥BF,F为垂足,
∴∠AFB=∠AEB=90°,
∴四边形AEBF为矩形;
点评 本题考查了矩形的判定、角平分线的定义、平角的定义等知识,解题的关键是掌握证明直角的方法,属于基础题,中考常考题型.

练习册系列答案
相关题目
2. 如图所示的几何体的左视图是( )
如图所示的几何体的左视图是( )
 如图所示的几何体的左视图是( )
如图所示的几何体的左视图是( )| A. |  | B. |  | C. |  | D. |  |
1.义务教育均衡发展是一种新的教育发展观,是解决我国目前教育问题的新举措.其最终目标,就是要合理配置教育资源,办好每一所学校,教好每一个学生,实现教育公平.我们县级政府为推进义务教育均衡发展工作的评估,今年预算办学经费约为3亿5千万,请你用科学记数法表示应是( )
| A. | 3.5×108 | B. | 3.5×109 | C. | 35×108 | D. | 0.35×109 |
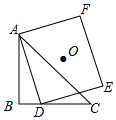 如图,△ABC中,∠ABC=90°,AB=BC=4,D为BC边上一动点,点O是正方形ADEF的中心,当点D沿BC边从点B运动到点C时,点O运动的路径长为2$\sqrt{2}$.
如图,△ABC中,∠ABC=90°,AB=BC=4,D为BC边上一动点,点O是正方形ADEF的中心,当点D沿BC边从点B运动到点C时,点O运动的路径长为2$\sqrt{2}$. 如图,四边形ADBC中,∠D、∠C为直角,G、I分别是△ABC、△ABD的内心,延长AG、BG、AI、BI交四边于Q、E、P、F,如果四边形GAIB的面积为17,求六边形EAFPBQ的面积.
如图,四边形ADBC中,∠D、∠C为直角,G、I分别是△ABC、△ABD的内心,延长AG、BG、AI、BI交四边于Q、E、P、F,如果四边形GAIB的面积为17,求六边形EAFPBQ的面积.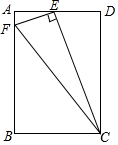 如图,在矩形ABCD中,E为AD上一点,EF⊥EC交AB于F,连接FC,△AEF与△DCE是否相似?请加以说明.
如图,在矩形ABCD中,E为AD上一点,EF⊥EC交AB于F,连接FC,△AEF与△DCE是否相似?请加以说明.