题目内容
8.先化简.再求值:(1-$\frac{1}{1-x}$)÷$\frac{x}{1-{x}^{2}}$,其中x=-$\frac{1}{2}$.分析 首先把括号内的分式通分相加,把除法转化为乘法,然后进行约分即可化简,最后代入数值计算即可.
解答 解:原式=$\frac{1-x-1}{1-x}$•$\frac{(1+x)(1-x)}{x}$
=-$\frac{x}{1-x}$•$\frac{(1+x)(1-x)}{x}$
=-(1+x)
=-1-x.
当x=-$\frac{1}{2}$时,原式=-1+$\frac{1}{2}$=-$\frac{1}{2}$.
点评 本题考查了分式的化简求值,正确对分式进行通分、约分是关键.

练习册系列答案
相关题目
18.下列运算正确的是( )
| A. | (a2)3=a5 | B. | a3•a=a4 | C. | (3ab)2=6a2b2 | D. | a6÷a3=a2 |
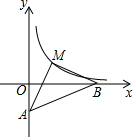 如图,直线y=$\frac{1}{5}$x-1与x轴、y轴分别相交于B、A,点M为双曲线y=$\frac{k}{x}$(x>0)上一点,若△AMB是以AB为底的等腰直角三角形,求S△MAB及k的值.
如图,直线y=$\frac{1}{5}$x-1与x轴、y轴分别相交于B、A,点M为双曲线y=$\frac{k}{x}$(x>0)上一点,若△AMB是以AB为底的等腰直角三角形,求S△MAB及k的值.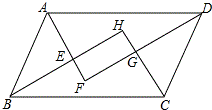 如图,平行四边形ABCD的四个内角的平分线分别相交于点E、F、G、H,求证:四边形EFGH是矩形.
如图,平行四边形ABCD的四个内角的平分线分别相交于点E、F、G、H,求证:四边形EFGH是矩形. 如图,四边形ADBC中,∠D、∠C为直角,G、I分别是△ABC、△ABD的内心,延长AG、BG、AI、BI交四边于Q、E、P、F,如果四边形GAIB的面积为17,求六边形EAFPBQ的面积.
如图,四边形ADBC中,∠D、∠C为直角,G、I分别是△ABC、△ABD的内心,延长AG、BG、AI、BI交四边于Q、E、P、F,如果四边形GAIB的面积为17,求六边形EAFPBQ的面积.