题目内容
11. 如图,在?ABCD中,AE⊥BC于E,AF⊥DC于F,∠ADC=60°,BE=2,CF=1,求?ABCD的面积.
如图,在?ABCD中,AE⊥BC于E,AF⊥DC于F,∠ADC=60°,BE=2,CF=1,求?ABCD的面积.
分析 根据平行四边形的性质即可求得∠B=60°,在直角三角形ABE中求得AB的长,同理求得AF的长,继而求得平行四边形ABCD的面积.
解答 解:∵四边形ABCD是平行四边形,∠ADC=60°,
∴∠B=∠D=60°,AB=CD,
∵AE⊥BC,AF⊥CD,
∴∠AEB=∠AEC=∠AFC=∠AFD=90°,
∴∠BAE=∠FAD=30°,
∵BE=2,FD=3cm,
∴AB=CD=4,
∴DF=3,
∴AF=3$\sqrt{3}$,
∴S平行四边形ABCD=CD•AF=4×3$\sqrt{3}$=12$\sqrt{3}$.
点评 此题考查了平行四边形的性质:平行四边形的对边平行且相等.还考查了直角三角形中30°角所对的直角边是斜边的一半.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
2. 如图所示的几何体的左视图是( )
如图所示的几何体的左视图是( )
 如图所示的几何体的左视图是( )
如图所示的几何体的左视图是( )| A. |  | B. |  | C. |  | D. |  |
6.已知k>1,b=k,a+c=2k2,ac=2k4-$\frac{1}{2}$k2,则以a,b,c为边的三角形是( )
| A. | 等边三角形 | B. | 等腰三角形 | C. | 直角三角形 | D. | 无法确定 |
1.义务教育均衡发展是一种新的教育发展观,是解决我国目前教育问题的新举措.其最终目标,就是要合理配置教育资源,办好每一所学校,教好每一个学生,实现教育公平.我们县级政府为推进义务教育均衡发展工作的评估,今年预算办学经费约为3亿5千万,请你用科学记数法表示应是( )
| A. | 3.5×108 | B. | 3.5×109 | C. | 35×108 | D. | 0.35×109 |
 一个正方体的每个面上都有一个汉字,其平面展开图如图所示,那么该正方体中与“价”字相对的字是( )
一个正方体的每个面上都有一个汉字,其平面展开图如图所示,那么该正方体中与“价”字相对的字是( )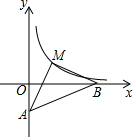 如图,直线y=$\frac{1}{5}$x-1与x轴、y轴分别相交于B、A,点M为双曲线y=$\frac{k}{x}$(x>0)上一点,若△AMB是以AB为底的等腰直角三角形,求S△MAB及k的值.
如图,直线y=$\frac{1}{5}$x-1与x轴、y轴分别相交于B、A,点M为双曲线y=$\frac{k}{x}$(x>0)上一点,若△AMB是以AB为底的等腰直角三角形,求S△MAB及k的值.