题目内容
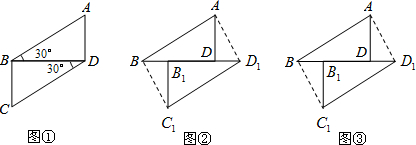
12.将两块全等的含30°角的三角尺如图①摆放在一起,设较短的直角边长为3.(1)四边形ABCD是平行四边形吗?说出你的结论和理由.
(2)如图②,将Rt△BCD沿射线BD方向平移到Rt△B1C1D1的位置,四边形ABC1D1是平行四边形吗?说出你的结论和理由.
(3)在Rt△BCD沿射线BD方向平移的过程中,当点B的移动距离为多少时四边形ABC1D1为矩形?
分析 (1)两组对边分别相等的四边形是平行四边形;
(2)有一组对边平行且相等的四边形是平行四边形;
(3)同(2)可证四边形ABC1D1是平行四边形,在此基础上,只要∠ABC1=90°,四边形ABC1D1就是矩形,即∠B1BC1=60°,然后利用勾股定理列方程计算.
解答 解:(1)是.如图①,
∵△ABD≌△CDB,
∴AD=BC,AB=CD,
∴四边形ABCD是平行四边形;
(2)是.如图②,
∵∠ABD=∠C1D1B1=30°
∴AB∥C1D1,
又∵AB=C1D1,
∴四边形ABC1D1是平行四边形;
(3)如图③,
由(2)知四边形ABC1D1是平行四边形
∴只要使∠ABC1=90°,四边形ABC1D1即为矩形
∴∠B1BC1=60°∴∠BC1B1=30°
设BB1=x,则 BC1=2x,
由勾股定理得:$B{C_1}^2-B{B_1}^2={B_1}{C_1}^2$,
即 (2x)2-x2=32
解得:$x=\sqrt{3}$,
∴当点B的移动距离为$\sqrt{3}$时四边形ABC1D1为矩形.
点评 本题考查了平移变换、全等三角形的判定与性质、平行四边形的判定与性质、矩形的判定与性质、勾股定理等知识点,难度适中.熟练掌握全等三角形、平行四边形、矩形的判定定理及性质定理是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 在直角三角形ABC中,BC=6,AC=8,点D在线段AC上从C向A运动.若设CD=x,△ABD的面积为y.
在直角三角形ABC中,BC=6,AC=8,点D在线段AC上从C向A运动.若设CD=x,△ABD的面积为y. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列四个结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列四个结论: