Question

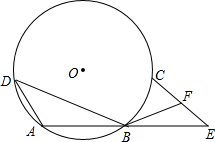如图，已知⊙O上依次有A、B、C、D四个点，

AD

=

BC

，连接AB、AD、BD，弦AB不经过圆心O，延长AB到E，使BE=AB，连接EC，F是EC的中点，连接BF．
（1）若⊙O的半径为3，∠DAB=120°，求劣弧

BD

的长；
（2）求证：BF=

1

2

BD；
（3）设G是BD的中点，探索：在⊙O上是否存在点P（不同于点B），使得PG=PF？并说明PB与AE的位置关系．

Answer 1

考点：圆的综合题

专题：几何综合题

分析：（1）利用圆心角定理进而得出∠BOD=120°，再利用弧长公式求出劣弧

BD

的长；
（2）利用三角形中位线定理得出BF=

1

2

AC，再利用圆心角定理得出

DAB

=

CBA

，进而得出BF=

1

2

BD；
（3）首先过点B作AE的垂线，与⊙O的交点即为所求的点P，得出BP⊥AE，进而证明△PBG≌△PBF（SAS），求出PG=PF．

解答：（1）解：连接OB，OD，
∵∠DAB=120°，∴

BCD

所对圆心角的度数为240°，
∴∠BOD=360°-240°=120°，
∵⊙O的半径为3，
∴劣弧

BD

的长为：

120

180

×π×3=2π；

（2）证明：连接AC，
∵AB=BE，∴点B为AE的中点，
∵F是EC的中点，∴BF为△EAC的中位线，
∴BF=

1

2

AC，
∵

AD

=

BC

，
∴

AD

+

AB

=

BC

+

AB

，
∴

DAB

=

CBA

，
∴BD=AC，
∴BF=

1

2

BD；

（3）解：过点B作AE的垂线，与⊙O的交点即为所求的点P，
∵BF为△EAC的中位线，
∴BF∥AC，
∴∠FBE=∠CAE，
∵

AD

=

BC

，
∴∠CAB=∠DBA，
∵由作法可知BP⊥AE，
∴∠GBP=∠FBP，
∵G为BD的中点，
∴BG=

1

2

BD，
∴BG=BF，
在△PBG和△PBF中，

BG=BF ∠PBG=∠PBF BP=BP

，
∴△PBG≌△PBF（SAS），
∴PG=PF．

点评：此题主要考查了圆的综合应用以及全等三角形的判定与性质和弧长公式以及圆心角定理等知识，正确作出辅助线是解题关键．