题目内容
 如图,一次函数y=kx+b的图象与反比例函数y=
如图,一次函数y=kx+b的图象与反比例函数y=| m |
| x |
(1)求一次函数、反比例函数的解析式;
(2)反比例函数图象上是否存在点D,使四边形BCPD为菱形?如果存在,求出点D的坐标;如果不存在,说明理由.
考点:反比例函数综合题
专题:综合题
分析:(1)由AC=BC,且OC⊥AB,利用三线合一得到O为AB中点,求出OB的长,确定出B坐标,从而得到P点坐标,将P与A坐标代入一次函数解析式求出k与b的值,确定出一次函数解析式,将P坐标代入反比例解析式求出m的值,即可确定出反比例解析式;
(2)假设存在这样的D点,使四边形BCPD为菱形,如图所示,由一次函数解析式求出C坐标,得出直线BC斜率,求出过P且与BC平行的直线PD解析式,与反比例解析式联立求出D坐标,检验得到四边形BCPD为菱形,符合题意.
(2)假设存在这样的D点,使四边形BCPD为菱形,如图所示,由一次函数解析式求出C坐标,得出直线BC斜率,求出过P且与BC平行的直线PD解析式,与反比例解析式联立求出D坐标,检验得到四边形BCPD为菱形,符合题意.
解答: 解:(1)∵AC=BC,CO⊥AB,A(-4,0),
解:(1)∵AC=BC,CO⊥AB,A(-4,0),
∴O为AB的中点,即OA=OB=4,
∴P(4,2),B(4,0),
将A(-4,0)与P(4,2)代入y=kx+b得:
,
解得:k=
,b=1,
∴一次函数解析式为y=
x+1,
将P(4,2)代入反比例解析式得:m=8,即反比例解析式为y=
;
(2)假设存在这样的D点,使四边形BCPD为菱形,如图所示,
对于一次函数y=
x+1,令x=0,得到y=1,即C(0,1),
∴直线BC的斜率为
=-
,
设过点P,且与BC平行的直线解析式为y-2=-
(x-4),即y=
,
与反比例解析式联立得:
,
消去y得:
=
,
整理得:x2-12x+32=0,即(x-4)(x-8)=0,
解得:x=4(舍去)或x=8,
当x=8时,y=1,
∴D(8,1),
此时PD=
=
,BC=
=
,即PD=BC,
∵PD∥BC,
∴四边形BCPD为平行四边形,
∵PC=
=
,即PC=BC,
∴四边形BCPD为菱形,满足题意,
则反比例函数图象上存在点D,使四边形BCPD为菱形,此时D坐标为(8,1).
 解:(1)∵AC=BC,CO⊥AB,A(-4,0),
解:(1)∵AC=BC,CO⊥AB,A(-4,0),∴O为AB的中点,即OA=OB=4,
∴P(4,2),B(4,0),
将A(-4,0)与P(4,2)代入y=kx+b得:
|
解得:k=
| 1 |
| 4 |
∴一次函数解析式为y=
| 1 |
| 4 |
将P(4,2)代入反比例解析式得:m=8,即反比例解析式为y=
| 8 |
| x |
(2)假设存在这样的D点,使四边形BCPD为菱形,如图所示,
对于一次函数y=
| 1 |
| 4 |
∴直线BC的斜率为
| 0-1 |
| 4-0 |
| 1 |
| 4 |
设过点P,且与BC平行的直线解析式为y-2=-
| 1 |
| 4 |
| -x+12 |
| 4 |
与反比例解析式联立得:
|
消去y得:
| -x+12 |
| 4 |
| 8 |
| x |
整理得:x2-12x+32=0,即(x-4)(x-8)=0,
解得:x=4(舍去)或x=8,
当x=8时,y=1,
∴D(8,1),
此时PD=
| (4-8)2+(2-1)2 |
| 17 |
| (4-0)2+(0-1)2 |
| 17 |
∵PD∥BC,
∴四边形BCPD为平行四边形,
∵PC=
| (4-0)2+(2-1)2 |
| 17 |
∴四边形BCPD为菱形,满足题意,
则反比例函数图象上存在点D,使四边形BCPD为菱形,此时D坐标为(8,1).
点评:此题属于反比例函数综合题,涉及的知识有:待定系数法确定函数解析式,一次函数与反比例函数的交点问题,坐标与图形性质,等腰三角形的性质,两点间的距离公式,两直线平行时斜率满足的关系,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2014年漳州市参加中考的学生数约49000人,这个数用科学记数法表示为( )
| A、4.9×103 |
| B、49×103 |
| C、4.9×104 |
| D、0.49×105 |
 如图,两块完全相同的含30°角的直角三角板ABC和A′B′C′重合在一起,将三角板A′B′C′绕其直角顶点C′按逆时针方向旋转角α(0<α≤90°),有以下四个结论:
如图,两块完全相同的含30°角的直角三角板ABC和A′B′C′重合在一起,将三角板A′B′C′绕其直角顶点C′按逆时针方向旋转角α(0<α≤90°),有以下四个结论:
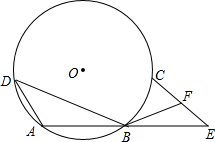 如图,已知⊙O上依次有A、B、C、D四个点,
如图,已知⊙O上依次有A、B、C、D四个点,