题目内容
已知梯形ABCD中，AD∥BC，MQ∥AD且分别交BD，AC于N，P，求证：MN=PQ．考点：平行线分线段成比例
专题：证明题
分析：先根据平行于三角形一边的直线截其他两边（或两边的延长线），所得的对应线段成比例由MQ∥AD得到
=
，
=
，再利用平行线分线段成比例得到
=
，则
=
，于是易得MN=PQ．
| MN |
| AD |
| BM |
| BA |
| PQ |
| AD |
| CQ |
| CD |
| BM |
| BA |
| CQ |
| CD |
| MN |
| AD |
| PQ |
| AD |
解答：证明：∵MQ∥AD，
∴
=
，
=
，
∵AD∥BC∥MQ，
∴
=
，
∴
=
，
∴MN=PQ．
∴
| MN |
| AD |
| BM |
| BA |
| PQ |
| AD |
| CQ |
| CD |
∵AD∥BC∥MQ，
∴
| BM |
| BA |
| CQ |
| CD |
∴
| MN |
| AD |
| PQ |
| AD |
∴MN=PQ．
点评：本题考查了平行线分线段成比例：三条平行线截两条直线，所得的对应线段成比例；平行于三角形一边的直线截其他两边（或两边的延长线），所得的对应线段成比例；如果一条直线截三角形的两边（或两边的延长线）所得的对应线段成比例，那这条直线平行于三角形的第三边．
练习册系列答案
高中必刷题系列答案
相关题目
梯形ABCD中，上底AD=8，下底BC=16，∠B=30°，∠C=60°，则腰长AB等于（ ）
A、4
| ||||
B、3
| ||||
C、5
| ||||
D、
|
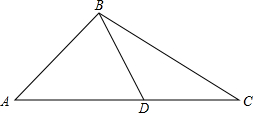如图，已知点D为△ABC中AC边上一点，AD=AB，BD=CD，4∠C=3∠A，试求∠A的度数．
已知：如图，△ABC中，AD平分∠BAC，且BD=CD，求证：∠B=∠C．