题目内容
已知|a|=4，|b|=6，且|a-b|=|a|+|b|，求ab和a-b的值．
考点：绝对值
专题：
分析：根据绝对值的性质求出a、b，再判断出a、b异号，然后代入代数式计算即可得解．
解答：解：∵|a|=4，|b|=6，
∴a=±4，b=±6，
∵|a-b|=|a|+|b|，
∴a、b异号，
∴a=4时，b=-6，
a=-4时，b=6，
∴ab=4×（-6）=-24，
或ab=（-4）×6=-24，
a-b=4-（-6）=4+6=10，
a-b=-4-6=-10．
∴a=±4，b=±6，
∵|a-b|=|a|+|b|，
∴a、b异号，
∴a=4时，b=-6，
a=-4时，b=6，
∴ab=4×（-6）=-24，
或ab=（-4）×6=-24，
a-b=4-（-6）=4+6=10，
a-b=-4-6=-10．
点评：本题考查了绝对值的性质，一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0，难点在于判断出a、b异号．
练习册系列答案
名牌中学课时作业系列答案
明天教育课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
周周清检测系列答案
相关题目
已知梯形ABCD中，AD∥BC，MQ∥AD且分别交BD，AC于N，P，求证：MN=PQ．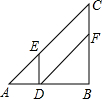
如图，在Rt△ABC中，AB=BC=12cm，点D从点A开始沿边AB以2cm/s的速度向点B移动，移动过程中始终保持DE∥BC，DF∥AC，问点D出发几秒后四边形DFCE的面积是△ABC面积的一半？
如图，如果从半径为5cm的圆形纸片上剪去