题目内容
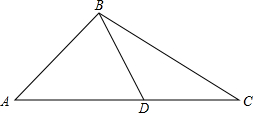 如图,已知点D为△ABC中AC边上一点,AD=AB,BD=CD,4∠C=3∠A,试求∠A的度数.
如图,已知点D为△ABC中AC边上一点,AD=AB,BD=CD,4∠C=3∠A,试求∠A的度数.考点:等腰三角形的性质
专题:
分析:先根据等腰三角形的性质和已知条件4∠C=3∠A,将∠C,∠CBD,∠ABD分别用∠C表示出来,根据三角形内角和定理可得关于∠A的方程,解方程即可求解.
解答:解:∵AD=AB,
∴∠ABD=90°-
∠A,
∵BD=CD,4∠C=3∠A,
∴∠C=∠CBD=
∠A,
∴∠A+90°-
∠A+
∠A+
∠A=180°,
解得∠A=45°.
故∠A的度数是45°.
∴∠ABD=90°-
| 1 |
| 2 |
∵BD=CD,4∠C=3∠A,
∴∠C=∠CBD=
| 3 |
| 4 |
∴∠A+90°-
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
解得∠A=45°.
故∠A的度数是45°.
点评:考查了等腰三角形的两个底角相等的性质,以及三角形内角和定理:三角形内角和等于180°.

练习册系列答案
相关题目
在数轴上到原点的距离6个单位长度的点表示的数为( )
| A、6 | B、-6 |
| C、6或-6 | D、不能确定 |
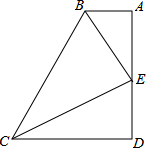 如图,BA⊥AD,CD⊥AD,垂足分别为A、D,BE,CE分别平分∠ABC、∠BCD,交点E恰好在AD上.BC=AB+CD是否成立?请说明理由.
如图,BA⊥AD,CD⊥AD,垂足分别为A、D,BE,CE分别平分∠ABC、∠BCD,交点E恰好在AD上.BC=AB+CD是否成立?请说明理由. 已知梯形ABCD中,AD∥BC,MQ∥AD且分别交BD,AC于N,P,求证:MN=PQ.
已知梯形ABCD中,AD∥BC,MQ∥AD且分别交BD,AC于N,P,求证:MN=PQ.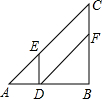 如图,在Rt△ABC中,AB=BC=12cm,点D从点A开始沿边AB以2cm/s的速度向点B移动,移动过程中始终保持DE∥BC,DF∥AC,问点D出发几秒后四边形DFCE的面积是△ABC面积的一半?
如图,在Rt△ABC中,AB=BC=12cm,点D从点A开始沿边AB以2cm/s的速度向点B移动,移动过程中始终保持DE∥BC,DF∥AC,问点D出发几秒后四边形DFCE的面积是△ABC面积的一半?