题目内容
解方程:
(1)x2-6x=0;
(2)x2-6x+9=(5-2x)2.
(1)x2-6x=0;
(2)x2-6x+9=(5-2x)2.
考点:解一元二次方程-因式分解法,解一元二次方程-配方法
专题:计算题
分析:(1)方程左边分解因式后,利用因式分解法求出解即可;
(2)方程左边变形后,开方即可求出解.
(2)方程左边变形后,开方即可求出解.
解答:解:(1)方程变形得:x(x-6)=0,
可得x=0或x-6=0,
解得:x1=0,x2=6;
(2)方程变形得:(x-3)2=(5-2x)2,
开方得:x-3=5-2x或x-3=2x-5,
解得:x1=
,x2=2.
可得x=0或x-6=0,
解得:x1=0,x2=6;
(2)方程变形得:(x-3)2=(5-2x)2,
开方得:x-3=5-2x或x-3=2x-5,
解得:x1=
| 8 |
| 3 |
点评:此题考查了解一元二次方程-因式分解法,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
相关题目
两个数的商是正数,那么这两个数( )
| A、和为正 | B、差为正 |
| C、积为正 | D、以上都不是 |
“
的平方根是±
”,用数学式子表示为( )
| 16 |
| 81 |
| 4 |
| 9 |
A、
| ||||||
B、±
| ||||||
C、
| ||||||
D、-
|
 已知:如图,在△ABC中,D是边BC上一点,BE⊥AD,CF⊥AD,垂足分别为E、F.
已知:如图,在△ABC中,D是边BC上一点,BE⊥AD,CF⊥AD,垂足分别为E、F.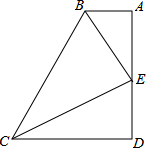 如图,BA⊥AD,CD⊥AD,垂足分别为A、D,BE,CE分别平分∠ABC、∠BCD,交点E恰好在AD上.BC=AB+CD是否成立?请说明理由.
如图,BA⊥AD,CD⊥AD,垂足分别为A、D,BE,CE分别平分∠ABC、∠BCD,交点E恰好在AD上.BC=AB+CD是否成立?请说明理由. 已知梯形ABCD中,AD∥BC,MQ∥AD且分别交BD,AC于N,P,求证:MN=PQ.
已知梯形ABCD中,AD∥BC,MQ∥AD且分别交BD,AC于N,P,求证:MN=PQ.