题目内容
13.当x$≠\frac{1}{2}$时,分式$\frac{x+1}{2x-1}$有意义.当x=-3时分式$\frac{{x}^{2}-9}{x-3}$的值为零.分析 根据分式有意义的条件可得2x-1≠0,再解方程即可;根据分式值为零的条件可得x2-9=0,且x-3≠0,再计算出x的值即可.
解答 解:由题意得:2x-1≠0,
解得:x≠$\frac{1}{2}$;
由题意得:x2-9=0,且x-3≠0,
解得:x=-3.
故答案为:≠$\frac{1}{2}$;=-3.
点评 此题主要考查了分式有意义和分式值为零的条件,关键是掌握分式有意义的条件是分母不等于零;分式值为零的条件是分子等于零且分母不等于零.
注意:“分母不为零”这个条件不能少.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案
相关题目
5.若△ABC∽△DEF,则AC=5,DF=1.5,则△ABC∽△DEF的相似比为( )
| A. | $\frac{3}{10}$ | B. | $\frac{10}{3}$ | C. | $\frac{7}{10}$ | D. | $\frac{10}{7}$ |
2.在下列几何体中,三视图中的三个视图的面积和的2倍与这个几何体的表面积有可能相等的有( )
①长方体;②三棱柱;③圆锥;④圆柱.
①长方体;②三棱柱;③圆锥;④圆柱.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
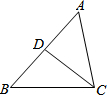 如图所示,给出下列条件:
如图所示,给出下列条件: