题目内容
16.已知点A(-3,0),B为直线y=x-2上一动点,求线段AB的最小值.分析 根据垂线段最短可知,当AB与直线y=x-2垂直时,线段AB最短,设直线y=x-2交x轴、y轴于C、D,根据交点坐标求得OC、OD、AC的长,然后根据△ABC∽△DOC,
即可求得AB的最小值.
解答  解:如图,根据垂线段最短,当AB与直线y=x-2垂直时,线段AB最短,
解:如图,根据垂线段最短,当AB与直线y=x-2垂直时,线段AB最短,
设直线y=x-2交x轴、y轴于C、D,
∴C(2,0),D(0,-2),
∴OC=2,OD=2,DC=2$\sqrt{2}$,
∵A(-3,0),
∴AC=5,
∵AB⊥BC,
∴∠ABC=90°,
∴∠ABC=∠DOC=90°,
∵∠ACB=∠DCO,
∴△ABC∽△DOC,
∴$\frac{AB}{OD}$=$\frac{AC}{CD}$,即$\frac{AB}{2}$=$\frac{5}{2\sqrt{2}}$,
∴AB=$\frac{5\sqrt{2}}{2}$.
∴线段AB的最小值为$\frac{5\sqrt{2}}{2}$.
点评 本题考查了一次函数图象上点的坐标特征,垂线段最短性质的应用,三角形相似的判定和性质,垂线段最短是本题的关键.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
8.下列各式中,与(2-$\sqrt{3}$)的积为有理数的是( )
| A. | 2$\sqrt{3}$ | B. | 2-$\sqrt{3}$ | C. | -2+$\sqrt{3}$ | D. | 2+$\sqrt{3}$ |
 已知,如图,P为△ABC内一点,请说明为什么∠BPC>∠BAC.(提示:联接AP,并延长到Q)
已知,如图,P为△ABC内一点,请说明为什么∠BPC>∠BAC.(提示:联接AP,并延长到Q)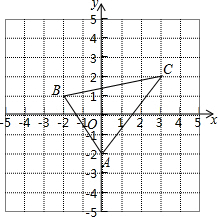 如图、已知A(0、-2)、B(-2、1)、C(3、2)
如图、已知A(0、-2)、B(-2、1)、C(3、2) 已知:如图,点B,E,C,F在一条直线上,AB∥DE,∠A=∠D,AC⊥BF,AC与DE相交于点M,对DF⊥BF说明理由.
已知:如图,点B,E,C,F在一条直线上,AB∥DE,∠A=∠D,AC⊥BF,AC与DE相交于点M,对DF⊥BF说明理由.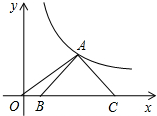 如图,等腰Rt△ABC的底边BC在x轴上,顶点A在双曲线y=$\frac{3}{x}$(x>0)上,连接OA,则OC2-OA2=( )
如图,等腰Rt△ABC的底边BC在x轴上,顶点A在双曲线y=$\frac{3}{x}$(x>0)上,连接OA,则OC2-OA2=( )